
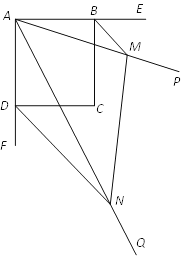
【题目】已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.
(1)求证:△ABM∽△NDA;
(2)连接BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.
【答案】(1)证明见解析;(2)22.5°.
【解析】试题分析:(1)由正方形ABCD,BM、DN分别是正方形的两个外角平分线,可证得∠ABM=∠ADN=135°,又由∠MAN=45°,可证得∠BAM=∠AND=45°-∠DAN,即可证得△ABM∽△NDA;
(2)由四边形BMND为矩形,可得BM=DN,然后由△ABM∽△NDA,根据相似三角形的对应边成比例,可证得BM2=AB2,继而求得答案.
试题解析:(1)证明:∵四边形ABCD是正方形,
∴∠ABC=∠ADC=∠BAD=90°,
∵BM、DN分别是正方形的两个外角平分线,
∴∠ABM=∠ADN=135°,
∵∠MAN=45°,
∴∠BAM=∠AND=45°-∠DAN,
∴△ABM∽△NDA;
(2)∵四边形BMND为矩形,
∴BM=DN,
∵△ABM∽△NDA,
∴![]() ,
,
∴BM2=AB2,
∴BM=AB,
∴∠BAM=∠BMA=![]()


科目:初中数学 来源: 题型:
【题目】两名同学在调查时使用的以下两种调查提问方式,你认为哪一种更好些?
①难道你不认为小说比诗歌更感人吗?
②你更喜欢哪一类文学作品——小说还是诗歌?
提问方式更好些的是________.(只需填问题代号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图所示,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
(2)自由下落的物体的高度h(米)与下落时间t(秒)的关系为h=4.9t2.有一学生不慎把一个玻璃杯从19.6米高的楼上掉下,刚好另有一学生站在与下落的玻璃杯同一直线的地面上,在玻璃杯下落的同时楼上的学生惊叫一声.则这时楼下的学生能躲开吗?(学生反应时间为1秒,声音的传播速度为340米/秒)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据“欢欢”与“乐乐”的对话,解决下面的问题:
欢欢:我手中有四张卡片,它们上面分别写有8,3x+2, ![]() x-3,
x-3, ![]() .
.
乐乐:我用等号将这四张卡片中的任意两张卡片上的数或式子连接起来,就会得到等式或一元一次方程.
问题:(1)乐乐一共能写出几个等式?
(2)在她写的这些等式中,有几个一元一次方程?请写出这几个一元一次方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,与y轴交于点C.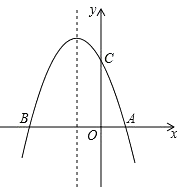
(1)求B、C两点的坐标;
(2)在该抛物线的对称轴上是否存在点P,使得△PAC的周长最小?若存在,求出点P的坐标;若不存在,请说明理由;
(3)抛物线在第二象限内是否存在一点Q,使△QBC的面积最大?,若存在,求出点Q的坐标及△QBC的面积最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用公式法解方程2x2﹣3x=1时,先求出a,b,c的值,则a,b,c依次是( )
A.2,3,1B.0,2,﹣3C.2,3,﹣1D.2,﹣3,﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx﹣4(a≠0)的图象与x轴交于A(﹣2,0)、C(8,0)两点,与y轴交于点B,其对称轴与x轴交于点D.
(1)求该二次函数的解析式;
(2)如图1,连结BC,在线段BC上是否存在点E,使得△CDE为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)如图2,若点P(m,n)是该二次函数图象上的一个动点(其中m>0,n<0),连结PB,PD,BD,求△BDP面积的最大值及此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题5分)某服装店老板以60元的单价购进20件流行款的女服装,老板交代销售小姐以80元为标准价出售.针对不同的顾客,销售小姐对20件服装的售价不完全相同,她把超过80元的记为正数,其销售结果如下表所示:

该服装店在售完这20件服装后,请你通过计算说明该服装店老板是赚钱还是亏本?如果赚钱,那么赚了多少钱?如果亏本,那么亏了多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com