
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y=ax2+bx��4��a��0����ͼ����x�ύ��A����2��0����C��8��0�����㣬��y�ύ�ڵ�B����Գ�����x�ύ�ڵ�D��
��1����ö��κ����Ľ���ʽ��
��2����ͼ1������BC�����߶�BC���Ƿ���ڵ�E��ʹ����CDEΪ���������Σ������ڣ�������з��������ĵ�E�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ2������P��m��n���Ǹö��κ���ͼ���ϵ�һ�����㣨����m��0��n��0��������PB��PD��BD������BDP��������ֵ����ʱ��P�����꣮

���𰸡���1��y=![]() x2��
x2��![]() x��4����2����8��2
x��4����2����8��2![]() ����
����![]() ������0����4������
������0����4������![]() ����
����![]() ������3����
������3����![]() ����
����![]() ����
����
�������������������1�����ݴ���ϵ�������ɵú�������ʽ��
��2���������ۣ���CD=DEʱ����EC=DEʱ����CD=CEʱ�����ݵ��������εĶ��壬�ɵù���m�ķ��̣����ݽⷽ�̣��ɵô𰸣�
��3����������ã���P������Ϊ��m�� ![]() m2-
m2-![]() m-4�����������ε������ʽ�������ε������ʽ���������BDP��������ݶ��κ��������ʽ��
m-4�����������ε������ʽ�������ε������ʽ���������BDP��������ݶ��κ��������ʽ��
�����������1���߶��κ���y=ax2+bx-4��a��0����ͼ����x�ύ��A��-2��0����C��8��0�����㣬
��![]() ��
��
���![]() ��
��
��ö��κ����Ľ���ʽΪy=![]() x2-
x2-![]() x-4��
x-4��
��2�����߶�BC���Ǵ��ڵ�E��ʹ����CDEΪ���������Σ�
�ɶ��κ���y=![]() x2-
x2-![]() x-4��֪�Գ���x=3��
x-4��֪�Գ���x=3��
��D��3��0����
��C��8��0����
��CD=5��
�ɶ��κ���y=![]() x2-
x2-![]() x-4��֪B��0��-4����
x-4��֪B��0��-4����
��BC�Ľ���ʽΪy=kx+b��
��B��C��������룬��
![]() ��
��
���![]() ��
��
BC�Ľ���ʽΪy=![]() x-4��
x-4��
E���߶�BC�ϣ���E������Ϊ��m�� ![]() m-4����
m-4����
�ٵ�CD=DEʱ������m-3��2+��![]() m-4��2=25�����m1=0��m2=8��������������ȥ����
m-4��2=25�����m1=0��m2=8��������������ȥ����
��m=0ʱ�� ![]() m-4=-4��
m-4=-4��
��E1��0��-4����
�ڵ�EC=DEʱ����m-8��2+��![]() m-4��2=��m-3��2+��
m-4��2=��m-3��2+��![]() m-4��2�����m3=
m-4��2�����m3=![]() ��
��
��m=![]() ʱ��
ʱ�� ![]() m-4=
m-4=![]() ��
��![]() -4=-
-4=-![]() ��
��
��E2��![]() ��-
��-![]() ����
����
�۵�CD=CEʱ����m-8��2+��![]() m-4��2=25�����m4=8+2
m-4��2=25�����m4=8+2![]() ��m5=8-2
��m5=8-2![]() �������������ᣩ��
�������������ᣩ��
��m=8+2![]() ʱ��
ʱ�� ![]() m-4=
m-4=![]() ����E3��8+2
����E3��8+2![]() ��
�� ![]() ����
����
�������������з��������ĵ�E������ΪE1��0��-4���� E2��![]() ��-
��-![]() ����E3��8+2
����E3��8+2![]() ��
�� ![]() ����
����
��3����P��������m�� ![]() m2-
m2-![]() m-4����
m-4����
y=![]() m2-
m2-![]() m-4=
m-4=![]() ��m-3��2-
��m-3��2-![]() ��
��
��BDP���=![]() ����4-
����4-![]() m 2+
m 2+![]() m-4����m-
m-4����m-![]() ��3��4-
��3��4-![]() ����m-3������-
����m-3������-![]() m2+
m2+![]() m+4��
m+4��
=-![]() m2+
m2+![]() m=-
m=-![]() ��m-
��m-![]() ��2+
��2+![]() ��
��
�൱m=![]() ʱ����BDP��������ʱ��P������Ϊ��
ʱ����BDP��������ʱ��P������Ϊ��![]() ��
�� ![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���в���ȷ������ ��
A. ����Ա߷ֱ�ƽ�е��ı�����ƽ���ı���
B. �Խ����ഹֱ��ƽ���ı���������
C. ��һ������ֱ�ǵ�ƽ���ı����Ǿ���
D. �����Խ����ഹֱ����ȵ��ı�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
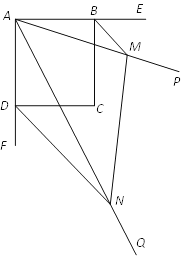
����Ŀ����֪����ͼ���ı���ABCD�������Σ���PAQ��45�㣬����PAQ���������εĶ���A��ת��ʹ����������ABCD��������ǡ�EBC�͡�FDC��ƽ���߷ֱ��ڵ�M��N������MN��
��1����֤����ABM�ס�NDA��
��2������BD������BAM�Ķ���Ϊ����ʱ���ı���BMNDΪ���Σ�������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪M��9x2��4x��3��N��5x2��4x��2����M��N�Ĵ�С��ϵ��(�� ��)
A. M>N B. M��N C. M<N D. ����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=1���Ҿ�����P��3��0��������������x�����һ����������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵxOy�У�ֱ��AC�ֱ���������A��C��8��0�����㣬AB��x�ᣬB��6��4����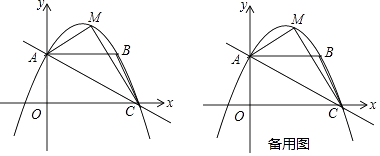
��1�����B��C�����������y=ax2+bx+4�ı���ʽ��
��2����P��C�������ÿ��1����λ���ٶ����߶�CO��O���˶���ͬʱ��Q��A���������ͬ���ٶ����߶�AB��B���˶�������һ�����㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮��tΪ��ֵʱ���ı���BCPQΪƽ���ı��Σ�
��3������MΪֱ��AC�Ϸ�����������һ���㣬����M�˶���ʲôλ��ʱ����AMC�������������ʱM�������͡�AMC����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һũ��Ҫ��һ���������ᣬ�����һ�����ó�Ϊ12m��ס��ǽ������������25m���Ľ�������Χ�ɣ�Ϊ����������ڴ�ֱ��ס��ǽ��һ����һ��1m�����ţ���Χ��������ij������ֱ�Ϊ����ʱ���������Ϊ80m2�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲μ�����ѧ�������˶���ijУ�����������10˫�˶�Ь����ͳ��10˫�˶�Ь�ĺ��루cm�������ʾ��
���� | 25 | 25.5 | 26 | 26.5 | 27 |
��������˫�� | 2 | 4 | 2 | 1 | 1 |
����10˫�˶�Ь�������������λ���ֱ��ǣ� ��
A.25.5cm 26cm
B.26cm 25.5cm
C.26cm 26cm
D.25.5cm 25.5cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ�������У�ÿ��С�����εı߳���Ϊ1.
(1)������ֱ������ϵ��ʹ��A������Ϊ(2����1)��
(2)��(1)�н�����ֱ������ϵ�������B(3��4)��C(0��1)������������ABC�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com