
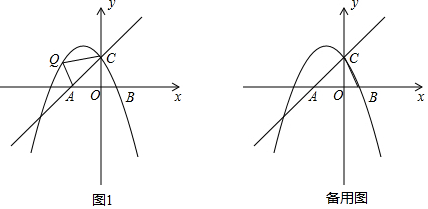
���� ��1������ֱ�ߵĽ���ʽ�õ���C��0��$\sqrt{3}$�����ѵ�B��1��0�����C��0��$\sqrt{3}$������y=-$\frac{\sqrt{3}}{3}$x2+bx+c�����ǵõ����ۣ�
��2��������OQ����ֱ��y=x+$\sqrt{3}$�У���y=0����x=-$\sqrt{3}$���õ���A��-$\sqrt{3}$��0�������������ε������ʽ���ɵõ����ۣ�
�ڽ�ֱ�������εõ���CBO=60�㣬��ֱ��ET����I�ڵ�T������FT�����EFT=90�㣬�õ�EF=ET•sin60��=$\frac{\sqrt{3}}{2}$ET����BD��ACʱ����ʱֱ��BD��С����ֱ��ET��С��EF��ֵ��С���Ƴ���CAO=45�㣬��Rt��ADB�У��������Ǻ����Ķ��弴�ɵõ����ۣ�
��� 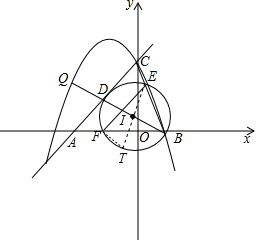 �⣺��1����ֱ��y=x+$\sqrt{3}$�У���x=0����y=$\sqrt{3}$��
�⣺��1����ֱ��y=x+$\sqrt{3}$�У���x=0����y=$\sqrt{3}$��
���C��0��$\sqrt{3}$����
�ѵ�B��1��0�����C��0��$\sqrt{3}$������y=-$\frac{\sqrt{3}}{3}$x2+bx+c���ã�$\left\{\begin{array}{l}c=\sqrt{3}\\-\frac{{\sqrt{3}}}{3}+b+c=0\end{array}\right.$��
��ã�$\left\{\begin{array}{l}b=-\frac{{2\sqrt{3}}}{3}\\ c=\sqrt{3}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=-$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x+$\sqrt{3}$��
��2��������OQ����ֱ��y=x+$\sqrt{3}$�У���y=0����x=-$\sqrt{3}$��
���A��-$\sqrt{3}$��0����
��S��AQC=S��AOQ+S��OCQ-S��AOC��
��S=$\frac{1}{2}��\sqrt{3}$��-$\frac{\sqrt{3}}{3}$t2-$\frac{2\sqrt{3}}{3}$t+$\sqrt{3}$��+$\frac{1}{2}$��$\sqrt{3}$•��-t��-$\frac{1}{2}��\sqrt{3}��\sqrt{3}$��
��S=-$\frac{1}{2}$t2-$\frac{2+\sqrt{3}}{2}$t����S=0$\frac{1}{2}$��t+$\frac{2+\sqrt{3}}{2}$��2+$\frac{7+4\sqrt{3}}{8}$����-3��t��0����
�൱t=-$\frac{2+\sqrt{3}}{2}$ʱ��${S_{���ֵ}}=\frac{{7+4\sqrt{3}}}{8}$��
�ڡߵ�B��1��0����C��0��$\sqrt{3}$������OB=1��OC=$\sqrt{3}$����
��Rt��BOC��tan��CBO=$\frac{OC}{OB}$=$\sqrt{3}$��
���CBO=60�㣬
��ֱ��ET����I�ڵ�T������FT�����EFT=90�㣬
�֡�FTE=��CBO=60�㣬sin��FTE=$\frac{EF}{ET}$��EF=ET•sin60��=$\frac{\sqrt{3}}{2}$ET��
��BD��ACʱ����ʱֱ��BD��С����ֱ��ET��С��EF��ֵ��С��
��Rt��AOC��OA=OC=$\sqrt{3}$��
���CAO=45�㣬
��Rt��ADB�У�BD=AB•sin��CAO=ABsin45��=|1-��-$\sqrt{3}$��|sin45��=$\frac{\sqrt{2}+\sqrt{6}}{2}$��
��EF=$\frac{\sqrt{3}}{2}$ET=$\frac{\sqrt{3}}{2}$BD=$\frac{\sqrt{3}}{2}$��$\frac{\sqrt{2}+\sqrt{6}}{2}$=$\frac{\sqrt{6}+3\sqrt{2}}{4}$��
��ʱ��Q������Ϊ��$\sqrt{3}$-3��4-$\sqrt{3}$����
���� ���⿼���˴���ϵ��������κ����Ľ���ʽ�����κ��������ʺ����ֵ����ֱ�������Σ������ε�����ļ��㣬��ȷ������ͼ���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
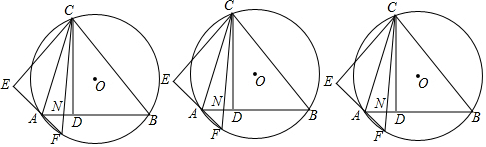
 ʵ����������ͼ����ABC��ֱ�������Σ���ACB=90�㣬����ֱ�ߺ�Բ�水����Ҫ����ͼ������ͼ�б�����Ӧ����ĸ����������ͼ�ۼ�����д������
ʵ����������ͼ����ABC��ֱ�������Σ���ACB=90�㣬����ֱ�ߺ�Բ�水����Ҫ����ͼ������ͼ�б�����Ӧ����ĸ����������ͼ�ۼ�����д�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪A��-4��n����B��2��-4����һ�κ���y=kx+b�ͷ���������y=$\frac{m}{x}$��ͼ����������㣮
��ͼ����֪A��-4��n����B��2��-4����һ�κ���y=kx+b�ͷ���������y=$\frac{m}{x}$��ͼ����������㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
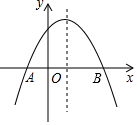 ��ͼ��������y=ax2+bx+c����x�ύ�ڵ�A��-1��0������������Ϊ��1��n������y�ύ���ڣ�0��2������0��3��֮�䣨�����˵㣩�������н��ۣ���abc��0����4ac-b2��0���۵�x=3ʱ��y=0����3a+b��0����-1��a��-$\frac{2}{3}$������$\frac{8}{3}$��n��4��������ȷ���У�������
��ͼ��������y=ax2+bx+c����x�ύ�ڵ�A��-1��0������������Ϊ��1��n������y�ύ���ڣ�0��2������0��3��֮�䣨�����˵㣩�������н��ۣ���abc��0����4ac-b2��0���۵�x=3ʱ��y=0����3a+b��0����-1��a��-$\frac{2}{3}$������$\frac{8}{3}$��n��4��������ȷ���У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
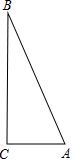
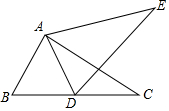 ��ͼ������ABC�Ƶ�A��ʱ����ת50��õ���ADE�����е�Dǡ������BC���ϣ����EDC���ڣ�������
��ͼ������ABC�Ƶ�A��ʱ����ת50��õ���ADE�����е�Dǡ������BC���ϣ����EDC���ڣ�������| A�� | 40�� | B�� | 50�� | C�� | 60�� | D�� | 65�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
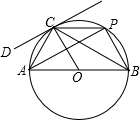 ��ͼ����C�ǰ뾶��Ϊ3�ġ�O������һ�㣬ABΪֱ����AC=3������C����O������DC����PΪ��O�Ż�AC�ϲ���A��C�غϵ�һ�����㣬��P�ӵ�C������ÿ��и���λ���ٶ�˳ʱ�������˶��������Aֹͣ�˶���
��ͼ����C�ǰ뾶��Ϊ3�ġ�O������һ�㣬ABΪֱ����AC=3������C����O������DC����PΪ��O�Ż�AC�ϲ���A��C�غϵ�һ�����㣬��P�ӵ�C������ÿ��и���λ���ٶ�˳ʱ�������˶��������Aֹͣ�˶����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
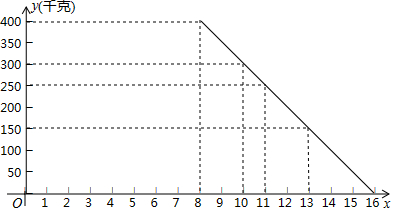
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
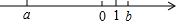 �������ϣ�ʵ��a��b��Ӧ�ĵ��λ����ͼ��ʾ�����н����У���ȷ���ǣ�������
�������ϣ�ʵ��a��b��Ӧ�ĵ��λ����ͼ��ʾ�����н����У���ȷ���ǣ�������| A�� | |a|��1 | B�� | |a|��1 | C�� | |b|��1 | D�� | ab��0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com