
分析 (1)易得原抛物线的顶点及平移后新抛物线的顶点,根据平移不改变二次项系数利用顶点式可得抛物线解析式;
(2)利用列表、描点、连线的方法作出两个函数的图象即可.
解答 解:(1)∵函数y=-$\frac{1}{2}$x2的顶点为(0,0),
∴向上平移2个单位,再向右平移1个单位的顶点为(1,2),
∴将函数y=-$\frac{1}{2}$x2的图象向上平移2个单位,再向右平移1个单位,得到抛物线的解析式为y=-$\frac{1}{2}$(x-1)2+2,
∴函数y=a(x-h)2+k中的a=-$\frac{1}{2}$,h=1,k=2;
(2)列表得:
| -2 | -1 | 0 | 1 | 2 | |
| y=-$\frac{1}{2}$x2 | 2 | $\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 2 |
| y=-$\frac{1}{2}$(x-1)2+2 | -$\frac{5}{2}$ | -1 | $\frac{3}{2}$ | 2 | $\frac{3}{2}$ |
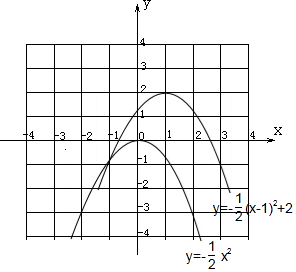 .
.点评 此题主要考查二次函数的平移情况;用到的知识点为:二次函数的平移不改变二次项的系数;关键是根据上下平移改变顶点的纵坐标,左右平移改变顶点的横坐标得到新抛物线的顶点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
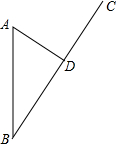 2016年9月中旬,全球最强台风“莫兰蒂”登陆福建,A市接到台风警报时,台风中心位于A市正南方向的B处,正以15km/h的速度沿BC方向移动.已知A市到BC的距离AD=30km,如果在距离台风中心45km(包括45km)的区域内都将受到台风影响,试问A市受到台风影响的时间是多长?( 结果精确到0.01h,参考数值:$\sqrt{5}$≈2.236 )
2016年9月中旬,全球最强台风“莫兰蒂”登陆福建,A市接到台风警报时,台风中心位于A市正南方向的B处,正以15km/h的速度沿BC方向移动.已知A市到BC的距离AD=30km,如果在距离台风中心45km(包括45km)的区域内都将受到台风影响,试问A市受到台风影响的时间是多长?( 结果精确到0.01h,参考数值:$\sqrt{5}$≈2.236 )查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
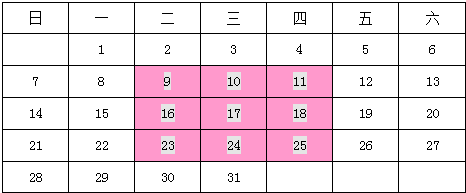
 我们可以用几何图形来解释一些代数恒等式,如图可以用来解释(a+b)2=a2+2ab+b2
我们可以用几何图形来解释一些代数恒等式,如图可以用来解释(a+b)2=a2+2ab+b2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com