
已知直线 分别与y轴、x轴相交于A、B两点,与二次函数
分别与y轴、x轴相交于A、B两点,与二次函数 的图像交于A、C两点.
的图像交于A、C两点.

(1)当点C坐标为( ,
, )时,求直线AB的解析式;
)时,求直线AB的解析式;
(2)在(1)中,如图,将△ABO沿y轴翻折180°,若点B的对应点D恰好落在二次函数 的图像上,求点D到直线AB的距离;
的图像上,求点D到直线AB的距离;
(3)当-1≤x≤1时,二次函数 有最小值-3,求实数m的值.
有最小值-3,求实数m的值.
(1)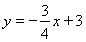 ;(2)4.8;(3)7或-7.
;(2)4.8;(3)7或-7.
【解析】
试题分析:(1)把C点坐标分别代入二次函数解析式,求出m的值;把A(0,b)代入二次函数解析式,求出b的值,再把C点坐标代入直线解析式,求出k的值,从而可求直线解析式;
(2)由(1)知点B的坐标,从而可确定点D的坐标,然后用面积法可求点D到直线AB的距离;
(3)进行分类讨论,分别求出m的值.
试题解析:(1)∵点C(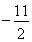 ,
,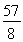 )在抛物线上,
)在抛物线上,
∴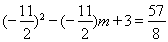
解得:m=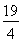 ,
,
∴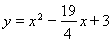
在直线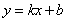 中,令x=0,则y=b,
中,令x=0,则y=b,
∴A(0,b)
把A点坐标代入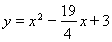 得,b=3
得,b=3
即A(0,3)
把(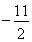 ,
,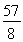 ),A(0,3)代入
),A(0,3)代入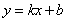 ,得
,得
 ,解得:
,解得: ,
,
所以直线AB的解析式为: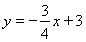 .
.
(2)令y=0,则x=4,故B(4,0)
∴D(-4,0).
连接CD,在△BCD中,BD=8,BC=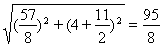
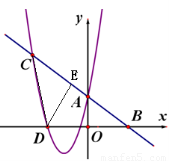
过D作DE⊥BC,垂足为E.则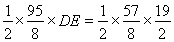 .
.
解得:DE=4.8
(3)∵抛物线的对称轴为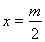 ,
,
∴当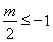 时,x=-1时二次函数的最小值为-3,得:
时,x=-1时二次函数的最小值为-3,得: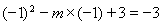 ,
,
解得:m=-7;
当-1<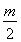 <1时,x=
<1时,x=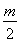 时二次函数的最小值为-3,得:
时二次函数的最小值为-3,得: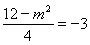 ,
,
解得:m=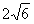 或
或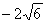 ,舍去.
,舍去.
当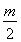 ≥1时,x=1时二次函数的最小值为-3,得:12-m+3=-3,解得:m=7;
≥1时,x=1时二次函数的最小值为-3,得:12-m+3=-3,解得:m=7;
所以实数m的值为7或-7.
考点: 二次函数综合题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 (2013•资阳)如图,已知直线l分别与x轴、y轴交于A,B两点,与双曲线y=
(2013•资阳)如图,已知直线l分别与x轴、y轴交于A,B两点,与双曲线y=| a | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
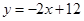 分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的圆M与直线AB相切于点D,连结MD.
分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的圆M与直线AB相切于点D,连结MD.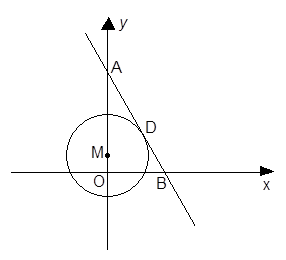

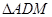 ∽
∽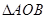 ;
;  ,请求出点M的坐标,并写出以
,请求出点M的坐标,并写出以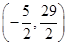 为顶点,且过点M的抛物线的解析式;
为顶点,且过点M的抛物线的解析式;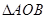 相似,如果存在,请求出所有符合条件的点P的坐标,如果不存在,请说明理由。
相似,如果存在,请求出所有符合条件的点P的坐标,如果不存在,请说明理由。查看答案和解析>>
科目:初中数学 来源:2012届浙江天门市实验初级中学九年级三轮考试数学卷(一)(带解析) 题型:解答题
如图,已知直线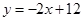 分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的圆M与直线AB相切于点D,连结MD.
分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的圆M与直线AB相切于点D,连结MD.
(1)求证:
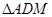 ∽
∽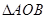 ;
;
(2)如果圆M的半径为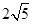 ,请求出点M的坐标,并写出以
,请求出点M的坐标,并写出以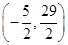 为顶点,且过点M的抛物线的解析式;
为顶点,且过点M的抛物线的解析式;
(3)在(2)的条件下,试问此抛物线上是否存在点P,使得以P、A、M三点为顶点的三角形与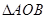 相似,如果存在,请求出所有符合条件的点P的坐标,如果不存在,请说明理由。
相似,如果存在,请求出所有符合条件的点P的坐标,如果不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2013年四川省资阳市中考数学试卷(解析版) 题型:解答题
 (a≠0,x>0)分别交于D、E两点.
(a≠0,x>0)分别交于D、E两点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com