
科目:初中数学 来源: 题型:
| 1 |
| x |
| 1 |
| x |
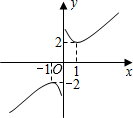 象似双钩,我们称之为“双钩函数”).给出下列几个命题:
象似双钩,我们称之为“双钩函数”).给出下列几个命题:查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 1 |
| x |
| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省泰兴市黄桥区九年级中考一模数学试卷(解析版) 题型:填空题
已知正比例函数 反比例函数
反比例函数 由
由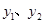 构造一个新函数
构造一个新函数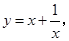 其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题:
其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题:
①该函数的图象是中心对称图形;
②当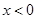 时,该函数在
时,该函数在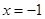 时取得最大值-2;
时取得最大值-2;
③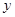 的值不可能为1;
的值不可能为1;
④在每个象限内,函数值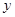 随自变量
随自变量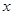 的增大而增大.
的增大而增大.
其中正确的命题是 .(请写出所有正确的命题的序号)
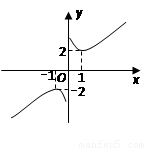
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com