Question

【题目】在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m），绘制出如下两幅统计图．请根据相关信息，解答下列问题：

（1）扇形统计图中a＝ ，初赛成绩为1.70m所在扇形图形的圆心角为

（2）补全条形统计图；

（3）这组初赛成绩的众数是 m，中位数是 ；

（4）根据这组初赛成绩确定8人进入复赛，那么初赛成绩为1.60m的运动员杨强能否进入复赛？为什么？

Answer 1

【答案】（1）15，72°．（2）补图见解析，（3）众数为1.60m，中位数为1.60m；（4）杨强不一定进入复赛．

【解析】试题分析：（1）用整体1减去其它所占的百分比，即可求出a的值；用360°乘以初赛成绩为1.70m所占的百分比即可；
（2）根据跳1.50m的人数和所占的百分比求出总人数，再乘以跳170m的人数所占的百分比，求出跳170m的人数，从而补全统计图；
（3）根据众数和中位数的定义分别进行解答即可；
（4）根据中位数的意义可直接判断出能否进入复赛．

试题解析：（1）根据题意得：
1-20%-10%-25%-30%=15%；
则a的值是15；
初赛成绩为1.70m所在扇形图形的圆心角为：360°×20%=72°；

（2）跳170m的人数是： ×20%=4（人），
补图如下：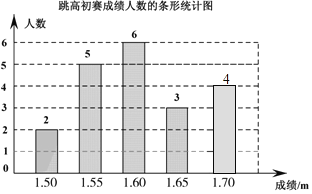

（3）∵在这组数据中，1.60m出现了6次，出现的次数最多，
∴这组数据的众数是1.60m；
将这组数据从小到大排列，其中处于中间的两个数都是1.60m，
则这组数据的中位数是1.60m．

（4）不一定，理由如下：
因为由高到低的初赛成绩中有4人是1.70m，有3人是1.65m，第8人的成绩为1.60m，但是成绩为1.60m的有6人，所以杨强不一定进入复赛．