Question

【题目】如图，菱形ABCD中，

（1）若半径为1的⊙O经过点A、B、D，且∠A＝60°，求此时菱形的边长；

（2）若点P为AB上一点，把菱形ABCD沿过点P的直线a折叠，使点D落在BC边上，利用无刻度的直尺和圆规作出直线a．（保留作图痕迹，不必说明作法和理由）

Answer 1

【答案】（1）菱形的边长为；

（2）作图见解析.

【解析】试题分析：（1）连接OB、OD和OC，根据菱形、内接圆的性质可得∠DOB＝120°，OD＝OB＝1， CD＝BC，∠C＝60°，从而得到△COD≌△COB，根据全等三角形的性质，可求得∠COD＝∠COB＝ 、∠DCO＝∠BCO＝，根据三角形内角和可得△COD 是Rt△COD，由tan∠DCO＝可求得CD的长度，即为所求；（2）根据题意先作出D在BC上的对应点；作出直线a；

试题解析：

(1)连接OB、OD和OC，如图所示：

∵半径为1的⊙O经过点A、B、D，且∠A＝60°，

∴∠DOB＝120°，OD＝OB＝1，

∵四边形ABCD是菱形，∠A＝60°，

∴CD＝BC，∠C＝60°，

在△COD和△COB中

∴△COD≌△COB（SSS），

∴∠COD＝∠COB，∠DCO＝∠BCO，

∴∠COD＝∠COB＝ ，

∠DCO＝∠BCO＝

∴∠ODC＝（180－30－60）o=90o,

∴△COD 是Rt△COD，

∵tan∠DCO＝

∴CD＝tan30o

∴菱形ABCD的边长是 ；

（2）如图所示：

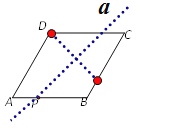
作出D在BC上的对应点，再作出直线a即可。