
【题目】如图,CD是△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处.

(1)求∠A的度数;
(2)若![]() ,求△AEC的面积.
,求△AEC的面积.
【答案】 (1)∠A的度数为30°; (2) △AEC面积为![]() .
.
【解析】分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得到AC=AE,从而得到∠A=∠ACE,再由折叠的性质及三角形的外角性质得到∠B=2∠A,从而不难求得∠A的度数.(2)由(1)得∠A=30°,据解直角三角形得△CEB是等边三角形,继而求解.
本题解析:(1)∵E是AB中点,∴CE为Rt△ACB斜边AB上的中线。AE=BE=CE=![]() AB,。
AB,。
∵CE=CB.∴△CEB为等边三角形。
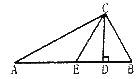
∴ ∠CEB=60°。 ∵ CE=AE.∴∠A=∠ACE=30°。
故∠A的度数为30°。
(2)∵Rt△ACB中,∠A=30°,∴tanA![]() ,
,
∴ AC=![]() ,BC=1,∴△CEB是等边三角形,CD⊥BE,∴CD=
,BC=1,∴△CEB是等边三角形,CD⊥BE,∴CD=![]() ,
,
∵AB=2BC=2,∴![]() ,∴S△ACE=
,∴S△ACE=![]() ,
,
即△AEC面积为![]() 。
。


科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的为8,B是数轴上一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
![]()
(1)写出数轴上点B表示的数 ,点P表示的数 (用含t的代数式表示);
(2)动点H从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、H同时出发,问点P运动多少秒时追上点H?
查看答案和解析>>
科目:初中数学 来源: 题型:
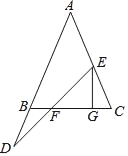
【题目】如图,∠ABC=∠C,点E在线段AC上,D在AB的延长线上,且有BD=CE,连接DE交BC于F,过E作FG⊥BC于G.试说明线段EF、FG、CG之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°. 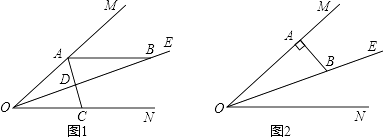
(1)如图1,若AB∥ON,则
①∠ABO的度数是;
②当∠BAD=∠ABD时,x=;当∠BAD=∠BDA时,x= .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,AB=3,BC=4.当平行四边形ABCD的面积最大时。下列结论正确的有( )
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
A.①②③
B.①②④
C.②③④
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,
(1)若半径为1的⊙O经过点A、B、D,且∠A=60°,求此时菱形的边长;
(2)若点P为AB上一点,把菱形ABCD沿过点P的直线a折叠,使点D落在BC边上,利用无刻度的直尺和圆规作出直线a.(保留作图痕迹,不必说明作法和理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知命题:等边三角形是等腰三角形.则下列说法正确的是( )
A. 该命题为假命题 B. 该命题为真命题
C. 该命题的逆命题为真命题 D. 该命题没有逆命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com