练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】（1）a（5a-3b）-（a-2b）

    （2）2（x2y-xy）-3（xy-x2y）-4x2y，其中x=-1．y=1．

    【答案】（1）5a2-3ab-a+2b；（2）6.

    【解析】

    （1）去括号即可；

    （2）先去括号合并同类项将式子化为最简形式，再把x、y的值代入计算即可．

    解： a（5a-3b）-（a-2b）

    =5a2-3ab-a+2b；

    （2）2（x2y-xy）-3（xy-x2y）-4x2y

    =2x2y-2xy-3xy+3x2y-4x2y

    =x2y-5xy，

    当x= -1，y=1时，

    原式=（-1）2×1-5×（-1）×1

    =1+5

    =6.

    故答案为：（1）5a2-3ab-a+2b；（2）6.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】线段AB=5，AB∥x轴，若A点坐标为（﹣1，3），则B点坐标为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分解因式：x2﹣x= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，A、B均在边长为1的正方形网格格点上．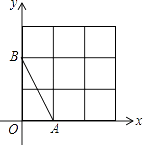

    （1）在网格的格点中，找一点C，使△ABC是直角三角形，且三边长均为无理数（只画出一个，并涂上阴影）；
    （2）若点P在图中所给网格中的格点上，△APB是等腰三角形，满足条件的点P共有个；
    （3）若将线段AB绕点A顺时针旋转90°，写出旋转后点B的坐标 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分解因式
    （1）4x3y﹣xy3
    （2）﹣x2+4xy﹣4y2 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=﹣x﹣4与抛物线y=ax2+bx+c相交于A，B两点，其中A，B两点的横坐标分别为﹣1和﹣4，且抛物线过原点．

    （1）求抛物线的解析式；

    （2）在坐标轴上是否存在点C，使△ABC为等腰三角形？若存在，求出点C的坐标，若不存在，请说明理由；

    （3）若点P是线段AB上不与A，B重合的动点，过点P作PE∥OA，与抛物线第三象限的部分交于一点E，过点E作EG⊥x轴于点G，交AB于点F，若S△BGF=3S△EFP，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市在创建全国文明城市过程中，决定购买A，B两种树苗对某路段道路进行绿化改造，已知购买A种树苗8棵，B种树苗3棵，需要950元；若购买A种树苗5棵，B种树苗6棵，则需要800元．

    （1）求购买A，B两种树苗每棵各需多少元？

    （2）考虑到绿化效果和资金周转，购进A种树苗不能少于50棵，且用于购买这两种树苗的资金不能超过7650元，若购进这两种树苗共100棵，则有哪几种购买方案？

    （3）某包工队承包种植任务，若种好一棵A种树苗可获工钱30元，种好一棵B种树苗可获工钱20元，在第（2）问的各种购买方案中，种好这100棵树苗，哪一种购买方案所付的种植工钱最少？最少工钱是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若2m-4与3m-1是同一个数的两个不等的平方根，则这个数是（ ）

    A. 2B. 一2C. 4D. 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=x2－4x与x轴交于O，A两点，P为抛物线上一点，过点P的直线y=x+m与对称轴交于点Q．

    （1）这条抛物线的对称轴是 ，直线PQ与x轴所夹锐角的度数是 ；

    （2）若两个三角形面积满足S△POQ=S△PAQ，求m的值；

    （3）当点P在x轴下方的抛物线上时，过点C（2，2）的直线AC与直线PQ交于点D，求：①PD＋DQ的最大值；②PDDQ的最大值．

    查看答案和解析>>

    同步练习册答案