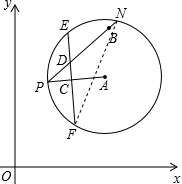
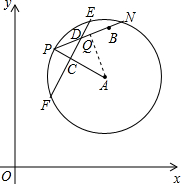
(1)证明:如图,连接NF,
∵CD⊥AP,
∴弧PE=弧PF,
又∵点E为劣弧PN的中点,
∴弧PE=弧NE,
∴弧EN=弧PF,
∴∠PNF=∠EFN,
∴DF=DN;
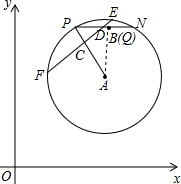
(2)解:如图,连接AE、AN,AE交PN于Q点,
∵弧PE=弧NE,
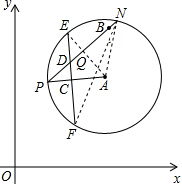
∴AE⊥PN,
∵CD⊥AP,
∴∠DCP=∠AQP=90°,
∴∠QAP=∠CDP,
∵PC:CA=2:3,不妨设⊙A的半径为5k,则CA=3k,AE=5k,
在Rt△ACE中,EC=
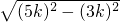
=4k,
∴tan∠CDP=tan∠EAC=
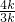
=

;
(3)解:过点A作AQ⊥PB于Q,如图,
∵⊙A的半径为5,PC:CA=2:3,
∴PC=2,
∵∠PCD=∠PQA=90°,
∴Rt△PCD∽Rt△PQA,
∴PD:PA=PC:PQ,
∴PD=
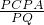
=
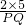
=
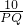
,
当PQ最小时,PD最大,
∵AQ≤AB,
∴AQ=AB时,AQ最大,此时AB⊥PB,
而PQ=
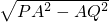
,
此时PQ最小,则PD最大,
又∵CD=

,
∴此时CD最大,
即AB⊥PB时,CD最大,如图,
而S
△APD=

AP•DC,
∴此时△APD的面积也达到最大,
∵点B的坐标为(6,9),点A的坐标为(6,6),
∴AB=3,
∴PB=

=4,
∴点P的坐标为(2,9),或(10,9).
分析:(1)连接NF,由CD⊥AP,根据垂径定理得到弧PE=弧PF,而弧PE=弧NE,则弧EN=弧PF,根据同弧或等弧所对的圆周角相等得到∠PNF=∠EFN,根据等腰三角形的性质即可得到结论;
(2)连接AE、AN,AE交PN于Q点,弧PE=弧NE,根据垂径定理的推论得到AE⊥PN,而CD⊥AP,则∠DCP=∠AQP=90°,根据等角的余角相等得到∠QAP=∠CDP,由PC:CA=2:3,不妨设⊙A的半径为5k,则CA=3k,AE=5k,在Rt△ACE中,根据勾股定理计算EC=
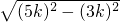
=4k,根据正切的定义即可得到tan∠CDP=tan∠EAC=
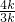
=

;
(3)过点A作AQ⊥PB于Q,由⊙A的半径为5,PC:CA=2:3,得到PC=2,易证Rt△PCD∽Rt△PQA,则PD:PA=PC:PQ,所以PD=
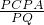
=
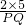
=
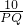
,当PQ最小时,PD最大,而AQ≤AB,则AQ=AB时,AQ最大,此时AB⊥PB,由PQ=
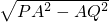
,得到此时PQ最小,则PD最大,又因为CD=

,得到此时CD最大,即AB⊥PB时,CD最大,由S
△APD=

AP•DC得到此时△APD的面积也达到最大,
由点B的坐标为(6,9),点A的坐标为(6,6),可得AB=3,利用勾股定理可计算出PB=4,于是可得到点P的坐标为(2,9),或(10,9).
点评:本题考查了圆的综合题:垂直于弦的直径平分弦,并且平分弦所对的弧;平分弦所对弧的直径垂直平分弦;在同圆或等圆中,同弧或等弧所对的圆周角相等;运用相似三角形的判定与性质可得到线段的比例关系;运用勾股定理和三角函数进行几何计算.

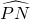 的中点时,求证:DF=DN;
的中点时,求证:DF=DN;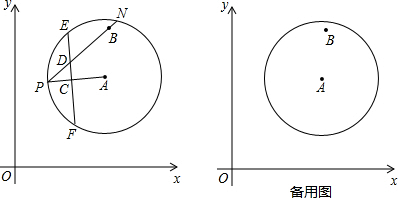
 (1)证明:如图,连接NF,
(1)证明:如图,连接NF,
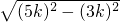 =4k,
=4k,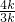 =
= ;
;
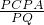 =
=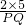 =
=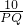 ,
,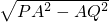 ,
, ,
, ∴此时CD最大,
∴此时CD最大, AP•DC,
AP•DC, =4,
=4,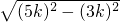 =4k,根据正切的定义即可得到tan∠CDP=tan∠EAC=
=4k,根据正切的定义即可得到tan∠CDP=tan∠EAC=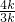 =
= ;
;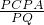 =
=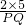 =
=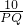 ,当PQ最小时,PD最大,而AQ≤AB,则AQ=AB时,AQ最大,此时AB⊥PB,由PQ=
,当PQ最小时,PD最大,而AQ≤AB,则AQ=AB时,AQ最大,此时AB⊥PB,由PQ=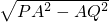 ,得到此时PQ最小,则PD最大,又因为CD=
,得到此时PQ最小,则PD最大,又因为CD= ,得到此时CD最大,即AB⊥PB时,CD最大,由S△APD=
,得到此时CD最大,即AB⊥PB时,CD最大,由S△APD= AP•DC得到此时△APD的面积也达到最大,
AP•DC得到此时△APD的面积也达到最大,

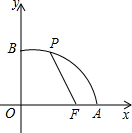 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-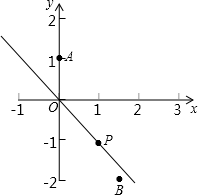 如图,已知点A的坐标为(0,1),点B的坐标为(
如图,已知点A的坐标为(0,1),点B的坐标为(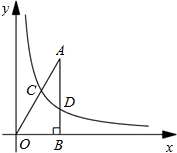 如图,已知点A的坐标为(
如图,已知点A的坐标为(

 如图,已知点A的坐标为(
如图,已知点A的坐标为(