
【题目】已知抛物线C:y=x2﹣2x+1的顶点为P,与y轴的交点为Q,点F(1, ![]() ).
).
(1)求点P,Q的坐标;
(2)将抛物线C向上平移得到抛物线C′,点Q平移后的对应点为Q′,且FQ′=OQ′.
①求抛物线C′的解析式;
②若点P关于直线Q′F的对称点为K,射线FK与抛物线C′相交于点A,求点A的坐标.
【答案】
(1)
解:∵y=x2﹣2x+1=(x﹣1)2
∴顶点P(1,0),
∵当x=0时,y=1,
∴Q(0,1)
(2)
解:①设抛物线C′的解析式为y=x2﹣2x+m,
∴Q′(0,m)其中m>1,
∴OQ′=m,
∵F(1, ![]() ),
),
过F作FH⊥OQ′,如图:
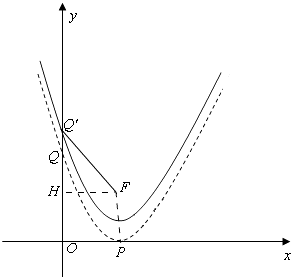
∴FH=1,Q′H=m﹣ ![]() ,
,
在Rt△FQ′H中,FQ′2=(m﹣ ![]() )2+1=m2﹣m+
)2+1=m2﹣m+ ![]() ,
,
∵FQ′=OQ′,
∴m2﹣m+ ![]() =m2,
=m2,
∴m= ![]() ,
,
∴抛物线C′的解析式为y=x2﹣2x+ ![]() ,
,
②设点A(x0,y0),则y0=x02﹣2x0+ ![]() ,
,
过点A作x轴的垂线,与直线Q′F相交于点N,则可设N(x0,n),
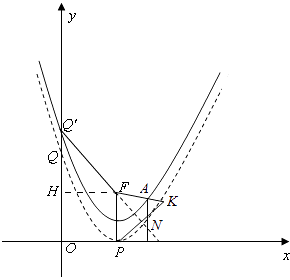
∴AN=y0﹣n,其中y0>n,
连接FP,
∵F(1, ![]() ),P(1,0),
),P(1,0),
∴FP⊥x轴,
∴FP∥AN,
∴∠ANF=∠PFN,
连接PK,则直线Q′F是线段PK的垂直平分线,
∴FP=FK,有∠PFN=∠AFN,
∴∠ANF=∠AFN,则AF=AN,
根据勾股定理,得,AF2=(x0﹣1)2+(y0﹣ ![]() )2,
)2,
∴(x0﹣1)2+(y0﹣ ![]() )2=(x
)2=(x ![]() ﹣2x0+
﹣2x0+ ![]() )+y
)+y ![]() ﹣y0=y
﹣y0=y ![]() ,
,
∴AF=y0,
∴y0=y0﹣n,
∴n=0,
∴N(x0,0),
设直线Q′F的解析式为y=kx+b,
则 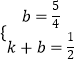 ,
,
解得 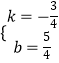 ,
,
∴y=﹣ ![]() x+
x+ ![]() ,
,
由点N在直线Q′F上,得,0=﹣ ![]() x0+
x0+ ![]() ,
,
∴x0= ![]() ,
,
将x0= ![]() 代入y0=x
代入y0=x ![]() ﹣2x0+
﹣2x0+ ![]() ,
,
∴y0= ![]() ,
,
∴A( ![]() ,
, ![]() )
)
【解析】此题是二次函数综合题,主要考查了待定系数法求解析式,线段的垂直平分线的判定和性质,解本题的关键是灵活运用勾股定理.(1)令x=0,求出抛物线与y轴的交点,抛物线解析式化为顶点式,求出点P坐标;(2)①设出Q′(0,m),表示出Q′H,根据FQ′=OQ′,用勾股定理建立方程求出m,即可.②根据AF=AN,用勾股定理,(x﹣1)2+(y﹣ ![]() )2=(x2﹣2x+
)2=(x2﹣2x+ ![]() )+y2﹣y=y2 , 求出AF=y,再求出直线Q′F的解析式,即可.
)+y2﹣y=y2 , 求出AF=y,再求出直线Q′F的解析式,即可.
【考点精析】根据题目的已知条件,利用线段垂直平分线的判定的相关知识可以得到问题的答案,需要掌握和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.
(1)求证:AC2=CDBC;
(2)过E作EG⊥AB,并延长EG至点K,使EK=EB.
①若点H是点D关于AC的对称点,点F为AC的中点,求证:FH⊥GH;
②若∠B=30°,求证:四边形AKEC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据直角三角形的判定的知识解决下列问题
(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°;
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点E为矩形ABCD边AD上一点,点P,点Q同时从点B出发,点P沿BE→ED→DC 运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P,Q出发t秒时,△BPQ的面积为ycm,已知y与t的函数关系的图形如图2(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5cm;②当0<t≤5时,![]() ;③直线NH的解析式为
;③直线NH的解析式为![]() ;④若△ABE与△QBP相似,则t=
;④若△ABE与△QBP相似,则t=![]() 秒。其中正确的结论个数为( )
秒。其中正确的结论个数为( )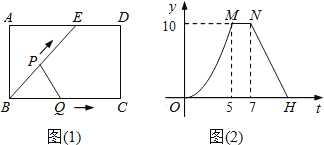
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( ) 
A.75°36′
B.75°12′
C.74°36′
D.74°12′
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com