

 GAE=450,
GAE=450,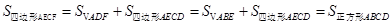 ,利用正方形的面积公式即可得到四边形BFDE的面积.
,利用正方形的面积公式即可得到四边形BFDE的面积. GAE=
GAE= GAF,从而得出△AEG≌△AGF,证出EG=GF=GD+BE;
GAF,从而得出△AEG≌△AGF,证出EG=GF=GD+BE;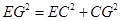 ,从而求出DG的长.
,从而求出DG的长.

科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
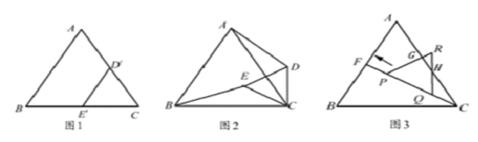
 满足0<º
满足0<º <90º,四边形CHGK是旋转过程中两块三角板的重叠部分(如图2).
<90º,四边形CHGK是旋转过程中两块三角板的重叠部分(如图2).
 ?若存在,请求出此时KC的长度;若不存在,请说明理由.
?若存在,请求出此时KC的长度;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.上午10点时,走在路上的人的影子 | B.晚上10点时,走在路灯下的人的影子 |
| C.中午用来乘凉的树影 | D.升国旗时,地上旗杆的影子 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.①②③ | B.①②④ | C.①③④ | D.②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com