
【题目】为宣传节约用水,小明随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如图所示的统计图.
(1)小明一共调查了多少户家庭?
(2)求所调查家庭5月份用水量的众数、平均数.
(3)若该小区有400户居民,请你估计这个小区5月份的用水量.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,AB=3,BC=4,E,F两点分别在边AB,BC上运动,△BEF沿EF折叠后为△GEF,
(1)若BF=a,则线段AG的最小值为 . (用含a的代数式表示)
(2)问:在E、F运动过程中,取a= 时,AG有最小值,值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为12,在其角上去掉两个全等的矩形DMNP和矩形BIJK,DM=IB=2,DP=BK=3,正方形EFGH顶点分别在正方形ABCD的边上,且EH过N点,则正方形EFGH的边长是( )
A.10
B.3 ![]()
C.4 ![]()
D.3 ![]() 或4
或4 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2x﹣3,点P在该函数的图象上,点P到x轴、y轴的距离分别为d1、d2 . 设d=d1+d2 , 下列结论中: ①d没有最大值;
②d没有最小值;
③﹣1<x<3时,d随x的增大而增大;
④满足d=5的点P有四个.
其中正确结论的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是![]() ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
A. 2,![]() B. 2,1 C. 4,
B. 2,1 C. 4,![]() D. 4,3
D. 4,3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB,CD相交于点O,AD,CB的延长线交于点E,OA=OC,EA=EC.
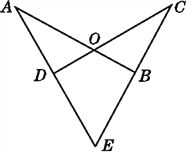
(1)试说明:∠A=∠C;
(2)在(1)的解答过程中,需要作辅助线,它的意图是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是过点
是过点![]() 的直线,
的直线,![]() 于
于![]() ,
,![]() 于点
于点![]() ;
;
(1)若![]() 、
、![]() 在
在![]() 的同侧(如图所示)且
的同侧(如图所示)且![]() .求证:
.求证:![]() ;
;
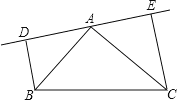
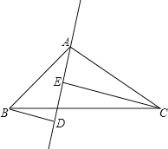
(2)若![]() 、
、![]() 在
在![]() 的两侧(如图所示),且
的两侧(如图所示),且![]() ,其他条件不变,
,其他条件不变,![]() 与
与![]() 仍垂直吗?若是请给出证明;若不是,请说明理由.
仍垂直吗?若是请给出证明;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,工人师傅常用“卡钳”这种工具测定工件内槽的宽.卡钳由两根钢条AA′、BB′组成,O为AA′、BB′的中点.只要量出A′B′的长度,由三角形全等就可以知道工件内槽AB的长度.则判定△OAB≌△OA′B′的依据是( )

A. SASB. ASAC. SSSD. AAS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:AC=AE;
(2)若点E为AB的中点,CD=4,求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com