
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是过点
是过点![]() 的直线,
的直线,![]() 于
于![]() ,
,![]() 于点
于点![]() ;
;
(1)若![]() 、
、![]() 在
在![]() 的同侧(如图所示)且
的同侧(如图所示)且![]() .求证:
.求证:![]() ;
;
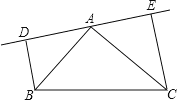
(2)若![]() 、
、![]() 在
在![]() 的两侧(如图所示),且
的两侧(如图所示),且![]() ,其他条件不变,
,其他条件不变,![]() 与
与![]() 仍垂直吗?若是请给出证明;若不是,请说明理由.
仍垂直吗?若是请给出证明;若不是,请说明理由.
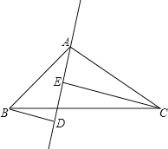
【答案】(1)见解析;(2)见解析.
【解析】
(1)由已知条件,证明ABD≌△CAE,再利用角与角之间的关系求证∠BAD+∠CAE=90°,即可证明AB⊥AC;
(2)同(1),先证ABD≌△CAE,再利用角与角之间的关系求证∠BAD+∠CAE=90°,即可证明AB⊥AC.
(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠ABC=∠90,
在Rt△ABD和Rt△CAE中,∵![]() ,
,
∴Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠ACE.
∵∠DAB+∠DBA=90,∠EAC+∠ACE=90,
∴∠BAD+∠CAE=90.
∠BAC=180-(∠BAD+∠CAE)=90.
∴AB⊥AC.
(2)AB⊥AC.理由如下:
同(1)一样可证得Rt△ABD=Rt△ACE.
∴∠DAB=∠ECA,∠DBA=∠EAC,
∵∠CAE+∠ECA=90°,
∴∠CAE+∠BAD=90,即∠BAC=90°,
∴AB⊥AC.



科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点. 如图①,若⊙O的半径为5,求线段OC的长;
如图②,过点A作AD∥BC交⊙O于点D,连接BD,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传节约用水,小明随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如图所示的统计图.
(1)小明一共调查了多少户家庭?
(2)求所调查家庭5月份用水量的众数、平均数.
(3)若该小区有400户居民,请你估计这个小区5月份的用水量.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,AC=BC,D是AB上的一点,AE⊥CD于点E,BF⊥CD于点F,若CE=BF,AE=EF+BF.试判断AC与BC的位置关系,并说明理由.
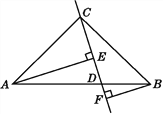
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲同学手中藏有三张分别标有数字 ![]() 、
、 ![]() 、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
(1)请你用树形图或列表法列出所有可能的结果;
(2)现制定一个游戏规则:若所选出的a,b能使得ax2+bx+1=0有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请用概率知识解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 | 6.7 | m | 3.41 | 90% | n |
八年级 | 7.1 | 7.5 | 1.69 | 80% | 10% |
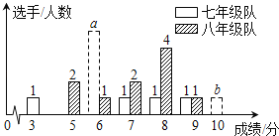
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
(1)如图1,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.求证:AE是△ABC的一条特异线.
(2)如图2,已知△ABC是特异三角形,且∠A=30°,∠B为钝角,求出所有可能的∠B的度数.
(3)如图3,△ABC是一个腰长为2的等腰锐角三角形,且它是特异三角形,若它的顶角度数为整数,请求出其特异线的长度;若它的顶角度数不是整数,请直接写出顶角度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com