
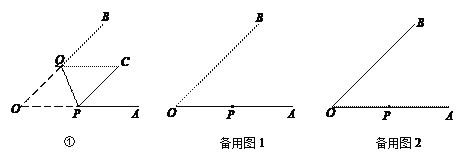
【题目】图①是一张∠AOB=45°的纸片折叠后的图形,P、Q分别是边OA、OB上的点,且OP=2 cm.将∠AOB沿PQ折叠,点O落在纸片所在平面内的C处.
(1)①当PC∥QB时,OQ= cm;
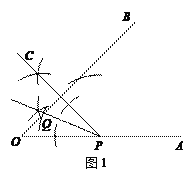
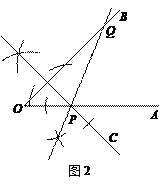
②在OB上找一点Q,使PC⊥QB(尺规作图,保留作图痕迹);
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.
【答案】(1)2;见解析(2)当点C在∠AOB的内部或一边上时,则重叠部分即为△CPQ
【解析】分析:(1)①证明四边形,即可得OQ=OP=2cm;②分点C、P在BQ同侧和异侧两种情况作图即可;(3)当折叠后重叠部分为等腰三角形时,符合条件的点Q共有5个;点C在∠AOB的内部或一边上时,由折叠的性质、三角形内角和定理以及解直角三角形即可求出OQ的长;点C在∠AOB的外部时,同理求出OQ的长即可.
详解:
(1)①当PC∥QB时,∠O=∠CPA,
由折叠的性质得:∠C=∠O,OP=CP,
∴∠CPA=∠C,
∴OP∥QC,
∴四边形OPCQ是平行四边形,
∴四边形OPCQ是菱形,
∴OQ=OP=2cm;
故答案为:2cm;
② 分点C、P在BQ同侧和异侧两种情况,画对一种就给全分;
(2)当点C在∠AOB的内部或一边上时,则重叠部分即为△CPQ.
因为△CPQ是由△OPQ折叠得到,所以当△OPQ为等腰三角形时,重叠部分必为等腰三角形.
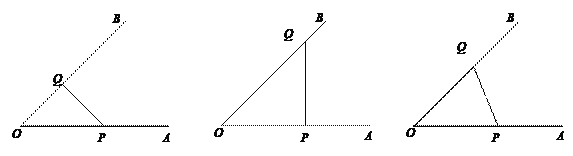 如图1、2、3三种情况:
如图1、2、3三种情况:
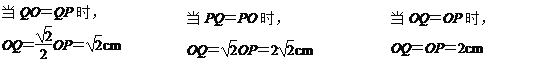

当点C在∠AOB的外部时,
当点C在射线OB的上方时(如图4), 当点C在射线OA的下方时(如图5),
OQ=![]() -
-![]() (cm)
(cm)
OQ=![]() +
+![]() (cm)
(cm)


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,E,F分别是正方形ABCD的边CD,AD上的点,CE=DF,AE,BF相交于点O.下列结论:①AE=BF;②AE⊥BF;③△ABF与△DAE成中心对称.其中,正确的结论有( )

A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠EDC=______°,∠AED=______°;
(2)线段DC的长度为何值时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,求∠BDA的度数;若不可以,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4 cm,则球的半径长是( )

A. 2cm B. 2.5cm C. 3cm D. 4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,一蔬菜经营户用180元钱从蔬菜批发市场批了西红柿和豆角共40千克到菜市场去卖,西红柿和豆角这天的批发价与零售价如下表所示:
品名 | 西红柿 | 豆角 |
批发价(单位:元/千克) | 3.6 | 4.6 |
零售价(单位:元/千克) | 5.4 | 7.5 |
问:他当天卖完这些西红柿和豆角能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)(2x+y)2﹣y(2x+y),其中x=![]() ,y=﹣1;
,y=﹣1;
(2)[(a﹣2b)2+(a﹣2b)(a+2b)﹣2a(2a﹣b)]÷2a,其中a=3,b=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=30cm,AC=40cm,点D在线段AB上,从点B出发,以2cm/s的速度向终点A运动,设点D的运动时间为t秒。

(1)点D在运动t秒后,BD= cm(用含有t的式子表示)
(2)AB=cm,AB边上的高为cm;
(3)点D在运动过程中,当△BCD为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家推行“节能减排,低碳经济”政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元,如图所示l1和l2分别表示每辆车的燃料费(含改装费)y(元)与正常运营时间x(天)之间的关系.

(1)哪条线表示每辆车改装后的燃料费(含改装费)y(元)与正常运营时间x(天)之间的关系?
(2)每辆车的改装费b= 元,正常营运 天后,就可以从节省的燃料费中收回改装成本;
(3)每辆车改装前每天的燃料费为 元;改装后每天的燃料费为 元;
(4)直接写出每辆车改装前、后的燃料费(含改装费)y(元)与正常运营时间x(天)之间的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com