练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    函数y="ax2+bx+c" (a、b、c是常数)，问当a、b、c满足什么条件时，   
    （1）它是二次函数？
    （2）它是一次函数？
    （3）它是正比例函数？

    ⑴当a≠0时；⑵当a=0且b≠0时；⑶当a=0，c=0， b≠0时。
    二次函数的定义：形如y＝ax2+bx+c(a≠0，a、b、c为常数)的函数叫做二次函数
    一次函数的定义：形式为y=ax+b形式的函数。其中a、b为常数，且a≠0
    正比例函数的定义：形如y=kx(k为常数，且k不等于0），y就叫做x的正比例函数
    根据各自的概念可以得出答案。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2013年初中毕业升学考试（河北卷）数学（解析版） 题型：解答题

    一透明的敞口正方体容器ABCD -A′B′C′D′ 装有一些液体，棱AB始终在水平桌面上，容器底部的倾斜角为α （∠CBE = α，如图1所示）．

    探究 如图1，液面刚好过棱CD，并与棱BB′ 交于点Q，此时液体的形状为直三棱柱，其三视图及尺寸如

    图2所示．解决问题：

    （1）CQ与BE的位置关系是       ，BQ的长是       dm；

    （2）求液体的体积；（参考算法：直棱柱体积V液 = 底面积SBCQ×高AB）

    （3）求α的度数.(注：sin49°＝cos41°＝，tan37°＝)

    拓展 在图1的基础上，以棱AB为轴将容器向左或向右旋转，但不能使液体溢出，图3或图4是其正面示意图.若液面与棱C′C或CB交于点P，设PC = x，BQ = y.分别就图3和图4求y与x的函数关系式，并写出相应的α的范围.

    延伸 在图4的基础上，于容器底部正中间位置，嵌入一平行于侧面的长方形隔板（厚度忽略不计），得到图5，隔板高NM =" 1" dm，BM = CM，NM⊥BC.继续向右缓慢旋转，当α = 60°时，通过计算，判断溢出容器的液体能否达到4 dm3.

     

    查看答案和解析>>

    科目：初中数学 来源：2014届河南省郑州市八年级下学期期中考试数学试卷（解析版） 题型：填空题

    如图，已知函数y =" 3x" + b和y =" ax" - 3的图象交于点P( -2，-5) ，则根据图象可得不等式3x + b ＞ax - 3的解集是                      .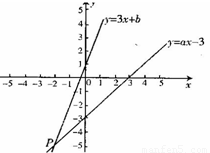

     

    查看答案和解析>>

    科目：初中数学 来源：2013年广东省广州市南沙区中考一模数学试卷（解析版） 题型：解答题

    如图1，已知抛物线与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，且OB =" 2OA" = 4．

    （1）求该抛物线的函数表达式；

    （2）设P是（1）中抛物线上的一个动点，以P为圆心，R为半径作⊙P，求当⊙P与抛物线的对称轴l及x轴均相切时点P的坐标．

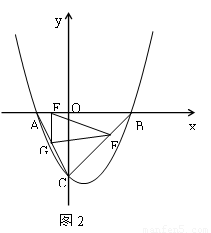
    （3）动点E从点A出发，以每秒1个单位长度的速度向终点B运动，动点F从点B出发，以每秒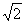个单位长度的速度向终点C运动，过点E作EG//y轴，交AC于点G（如图2）．若E、F两点同时出发，运动时间为t．则当t为何值时，△EFG的面积是△ABC的面积的？

     

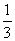    查看答案和解析>>

    科目：初中数学 来源：2013年重庆市八年级下学期阶段定时作业（一）数学卷（解析版） 题型：解答题

    已知函数y ="(2m+1)" x+ m-3

    (1) 若函数图象经过原点,求m的值

    (2) 若函数图象在y轴的交点的纵坐标为－2，求m的值

    （3）若函数的图象平行直线y=3x–3，求m的值  

    （4）若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.

     

    查看答案和解析>>

    同步练习册答案