
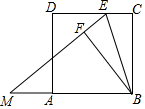
 如图,E为正方形ABCD的边DC上一点,DE=2EC=2,将△BEC沿BE所在的直线对折得到△BEF,延长EF交BA的延长线于点M,则AM=2.
如图,E为正方形ABCD的边DC上一点,DE=2EC=2,将△BEC沿BE所在的直线对折得到△BEF,延长EF交BA的延长线于点M,则AM=2. 分析 设AM=x.由题意BA=BC=CD=BF=3,CE=EF=2,由翻折得到∠BEC=∠BEF=∠EBM,推出MB=ME=x+3,在Rt△BFM中,由BM2=MF2+BF2,可得(x+3)2=32+(x+2)2,解方程即可.
解答  解:设AM=x.
解:设AM=x.
∵DE=2EC=2,
∴DE=2,EC=1,
∴CD=3,
∵四边形ABCD是正方形,
∴AB=BC=CD=3,CD∥AB,∠C=90°
∵△BEF是由△BEC翻折得到,
∴∠BEC=∠BEF=∠EBM,EC=EF=1,∠EFB=∠C=90°,
∴BM=EM=3+x,FM=x+2,
在Rt△BFM中,∵BM2=MF2+BF2,
∴(x+3)2=32+(x+2)2,
∴x=2,
∴AM=2.
故答案为2.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了正方形的性质和勾股定理.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
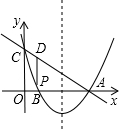 如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从点C沿抛物线向A点运动(运动到A点停止),过点P作PD∥y轴交直线AC于点D.
如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从点C沿抛物线向A点运动(运动到A点停止),过点P作PD∥y轴交直线AC于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
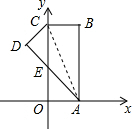 如图,在直角坐标系中,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为( )
如图,在直角坐标系中,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为( )| A. | (-$\frac{1}{2}$,$\frac{13}{5}$) | B. | (-$\frac{2}{5}$,$\frac{13}{5}$) | C. | (-$\frac{4}{5}$,$\frac{12}{5}$) | D. | (-$\frac{3}{5}$,$\frac{12}{5}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com