Question

19．如图，一个Rt△DEF直角边DE落在AB上，过A点作射线AC与斜边EF平行，已知AB=12，DE=4，DF=3，点P从A点出发，沿射线AC方向以每秒2个单位的速度运动，Q为AP中点，设运动时间为t秒（t＞0）
（1）若点D与点B重合，当t=5时，连接QE，PF，此时△AQE为等腰三角形、四边形QEFP为菱形；
（2）如图②，若在点P运动时，Rt△DEF同时沿着BA方向以每秒1个单位的速度运动，当D点到A点时，两个运动都停止．
①如图①，若M为EF中点，当D、M、Q三点在同一直线上时，求t的值；
②在运动过程中，以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切时，求运动时间t．

Answer 1

分析 （1）过点Q作QH⊥AB于H，如图①，易得PQ=EF=5，由AC∥EF可得四边形EFPQ是平行四边形，易证△AHQ∽△EDF，从而可得AH=ED=4，进而可得AH=HE=4，根据垂直平分线的性质可得AQ=EQ，即可得到PQ=EQ，即可得到平行四边形EFPQ是菱形；
（2）①当D、M、Q三点在同一直线上时，如图②，则有AQ=t，EM=$\frac{1}{2}$EF=$\frac{5}{2}$，AD=12-t，DE=4．由EF∥AC可得△DEM∽△DAQ，然后运用相似三角形的性质就可求出t的值；
②若以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切，则点Q在∠ADF的角平分线上（如图③）或在∠FDB的角平分线（如图④）上，故需分两种情况讨论，然后运用相似三角形的性质求出AH、DH（用t表示），再结合AB=12，DB=t建立关于t的方程，然后解这个方程就可解决问题．

解答 解：（1）四边形EFPQ是菱形．
理由：过点Q作QH⊥AB于H，如图①，
∵t=5，∴AP=2×5=10．
∵点Q是AP的中点，
∴AQ=PQ=5．
∵∠EDF=90°，DE=4，DF=3，
∴EF=$\sqrt{D{E}^{2}+D{F}^{2}}$=5，
∴PQ=EF=5．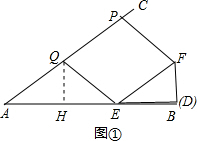
∵AC∥EF，
∴四边形EFPQ是平行四边形，且∠A=∠FEB．
又∵∠QHA=∠FDE=90°，
∴△AHQ∽△EDF，
∴$\frac{QH}{FD}$=$\frac{AH}{ED}$=$\frac{AQ}{EF}$．
∵AQ=EF=5，
∴AH=ED=4．
∵AE=12-4=8，
∴HE=8-4=4，
∴AH=EH，
∴AQ=EQ，
∴PQ=EQ，
∴△AQE是等腰三角形，平行四边形EFPQ是菱形；
故答案为：等腰，菱形．

（2）①当D、M、Q三点在同一直线上时，如图②，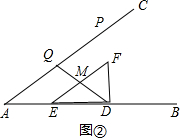
此时AQ=t，EM=$\frac{1}{2}$EF=$\frac{5}{2}$，AD=12-t，DE=4．
∵EF∥AC，
∴△DEM∽△DAQ，
∴$\frac{EM}{AQ}$=$\frac{DE}{DA}$，
∴$\frac{\frac{5}{2}}{t}$=$\frac{4}{12-t}$，
解得t=$\frac{60}{13}$；
②存在以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切，
此时点Q在∠ADF的角平分线上或在∠FDB的角平分线上．
Ⅰ．当点Q在∠ADF的角平分线上时，
过点Q作QH⊥AB于H，如图③，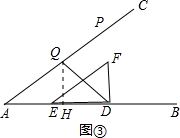
则有∠HQD=∠HDQ=45°，
∴QH=DH．
∵△AHQ∽△EDF（已证），
∴$\frac{QH}{FD}$=$\frac{AH}{ED}$=$\frac{AQ}{EF}$，
∴$\frac{QH}{3}$=$\frac{AH}{4}$=$\frac{t}{5}$，
∴QH=$\frac{3t}{5}$，AH=$\frac{4t}{5}$，
∴DH=QH=$\frac{3t}{5}$．
∵AB=AH+HD+BD=12，DB=t，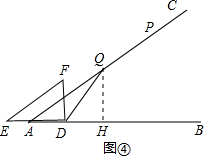
∴$\frac{4t}{5}$+$\frac{3t}{5}$+t=12，
∴t=5；
Ⅱ．当点Q在∠FDB的角平分线上时，
过点Q作QH⊥AB于H，如图④，
同理可得DH=QH=$\frac{3t}{5}$，AH=$\frac{4t}{5}$．
∵AB=AD+DB=AH-DH+DB=12，DB=t，
∴$\frac{4t}{5}$-$\frac{3t}{5}$+t=12，
∴t=10．
综上所述：当t为5秒或10秒时，以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切．

点评 本题主要考查了菱形的判定与性质、相似三角形的判定与性质、圆的切线的性质、等角对等边、勾股定理、垂直平分线的性质、解方程等知识，需要注意的是：到两条直线的距离相等的点在两条直线所成两组对顶角的角平分线上，避免出现漏解的现象．