Question

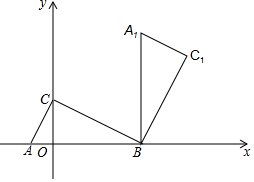
13．如图，在平面直角坐标系中，△ABC三个顶点坐标分别为A（-1，0）、B（4，0）、C（0，2），将△ABC绕点B顺时针旋转90°得到△A₁BC₁，有一条抛物线经过点A，且它的顶点为A₁．
（1）求该抛物线的解析式；
（2）该抛物线是否经过点C₁，请说明理由；
（3）在抛物线的对称轴上是否存在一点Q，|QC-QC₁|有最大值，若存在，请求出点Q的坐标，若不存在，请说明理由．

Answer 1

分析 （1）根据旋转的性质，可得顶点坐标，根据待定系数法，可得函数解析式；
（2）根据全等三角形的判定与性质，可得C₁，根据点的坐标满足函数解析式，点在函数图象上，可得答案；
（3）根据线段垂直平分线的性质，可得C₂，根据三角形的性质，可得Q在直线CC₂，根据自变量与函数值的对应关系，可得答案．

解答 解：（1）∵点A（-1，0），B（4，0），
∴AB=5得抛物线顶点A₁（4，5）
设该抛物线解析式为y=a（x-4）²+5
将点A（-1，0）代入，解得a=-$\frac{1}{5}$
∴该抛物线的解析式y=-$\frac{1}{5}$（x-4）²+5；
（2）过点C₁作C₁D⊥A₁B于点D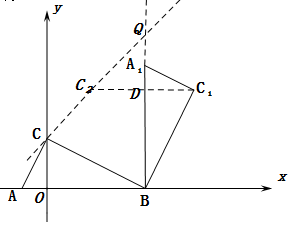
，
∴∠C₁DB=∠COB=90°
在△C₁DB和△COB中，
$\left\{\begin{array}{l}{{C}_{1}BD=CBO}\\{{C}_{1}DB=∠COB}\\{{C}_{1}B=CB}\end{array}\right.$
∴△C₁DB≌△CBO
∴BD=BO=4，C₁D=CO=2
∴C₁（6，4）
将x=6代入抛物线解析式求得$y=\frac{21}{5}≠4$，
∴抛物线不经过点C₁；
（3）延长C₁D至点C₂，使C₂D=C₁D，利用对称性，得到点C₂（2，4）
连接CC₂，并延长使它与直线A₁B交于点Q，
∵三角形两边之差小于第三边
∴此时|QC-QC₁|有最大值为CC₂的长；
求得：直线CC₂的解析式为y=x+2
∴当x=4时，求得点Q（4，6）．

点评 本题考查了二次函数综合题，解（1）的关键是待定系数法，解（2）的关键是利用全等三角形的判定与性质得出C₁的坐标；解（3）的关键是利用三角形的性质得出Q在直线CC上，又利用了线段垂直平分线的性质．