
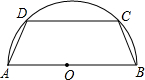
 如图,有一块半径为5cm的半圆形钢板,计划截成等腰梯形ABCD的形状,他的下底AB是⊙O的直径,上底CD的端点在圆周上.
如图,有一块半径为5cm的半圆形钢板,计划截成等腰梯形ABCD的形状,他的下底AB是⊙O的直径,上底CD的端点在圆周上.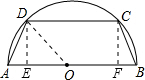 (1)过点D作DE⊥AB,CF⊥AB,连接OD,
(1)过点D作DE⊥AB,CF⊥AB,连接OD, =3cm,
=3cm,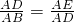 ,即
,即 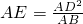 .
.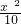 cm,
cm,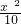 =(10-
=(10-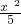 )cm,
)cm,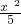 +x=-
+x=- +2x+20,
+2x+20,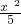 >0,10-
>0,10-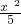 >0,
>0, ;
; +2x+20=-
+2x+20=- (x-5)2+25,
(x-5)2+25,

科目:初中数学 来源: 题型:
 |
| AB |
 |
| AC |
 部分).
部分).查看答案和解析>>
科目:初中数学 来源: 题型:
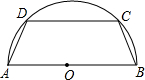 (2007•安溪县质检)如图,有一块半径为5cm的半圆形钢板,计划截成等腰梯形ABCD的形状,他的下底AB是⊙O的直径,上底CD的端点在圆周上.
(2007•安溪县质检)如图,有一块半径为5cm的半圆形钢板,计划截成等腰梯形ABCD的形状,他的下底AB是⊙O的直径,上底CD的端点在圆周上.查看答案和解析>>
科目:初中数学 来源:2012届江苏省南京市江宁区九年级中考二模数学试卷(带解析) 题型:解答题
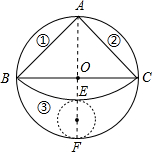
如图,有一块圆形铁皮,BC是⊙O的直径,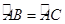 ,在此圆形铁皮中剪下一个扇形(阴影部分).
,在此圆形铁皮中剪下一个扇形(阴影部分).
(1)当⊙O的半径为2时,求这个扇形(阴影部分)的面积(结果保留 );
);
(2)当⊙O的半径为R(R>0)时,在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形
围成一个圆锥?请说明理由.
查看答案和解析>>
科目:初中数学 来源:2007年福建省泉州市安溪县初中学业质量检查数学试卷(解析版) 题型:解答题
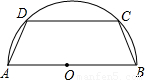
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com