
【题目】在平面直角坐标系中有点M(m,2m+3).
(1)若点M在x轴上,求m的值;
(2)若点M在第三象限内,求m的取值范围;
(3)点M在第二、四象限的角平分线上,求m的值.
【答案】
(1)解:∵M(m,2m+3)在x轴上,
∴2m+3=0,
∴m=﹣ ![]()
(2)解:∵M(m,2m+3)在第三象限内,
∴ ![]() ,
,
∴m<﹣ ![]()
(3)解:∵M(m,2m+3)在第二、四象限的角平分线上,
∴m+(2m+3)=0
∴m=﹣1.
【解析】(1)根据点在x轴上纵坐标为0,建立方程求解。
(2)根据点在第三象限横坐标,纵坐标都小于0,建立不等式组求解即可。
(3)根据第二、四象限的角平分线上的横坐标,纵坐标互为相反数,即横纵坐标之和=0,建立方程求解即可。
【考点精析】解答此题的关键在于理解解一元一次方程的步骤的相关知识,掌握先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了,以及对一元一次不等式组的解法的理解,了解解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).


科目:初中数学 来源: 题型:
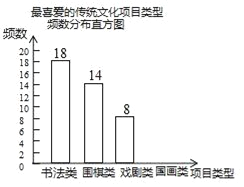
【题目】某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表
项目类型 | 频数 | 频率 |
书法类 | 18 | a |
围棋类 | 14 | 0.28 |
喜剧类 | 8 | 0.16 |
国画类 | b | 0.20 |
根据以上信息完成下列问题:
(1)频数分布表中a=_____,b=_____;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次知识竞赛中,甲、乙两人进入到“必答题”环节.规则是:两人轮流答题,每人都要回答20道题,每道题回答正确得![]() 分,回答错误或放弃回答扣
分,回答错误或放弃回答扣![]() 分.当甲、乙两人恰好都答完12道题时,甲答对了9道题,得分为39分;乙答对了10道题,得分为46分.
分.当甲、乙两人恰好都答完12道题时,甲答对了9道题,得分为39分;乙答对了10道题,得分为46分.
(1)求![]() 和
和![]() 的值;
的值;
(2)规定此环节得分不低于60分能晋级,甲在剩下的比赛中至少还要答对多少道题才能顺利晋级?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形的周长为11cm,其中一边长为3cm,则该等腰三角形的底长为( )
A. 3cm或5cm B. 3cm或4cm C. 3cm D. 5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2.善于思考的小明进行了以下探索:
)2.善于思考的小明进行了以下探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() .
.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =
=![]() ,用含m、n的式子分别表示a、b,得:a=__,b=__;
,用含m、n的式子分别表示a、b,得:a=__,b=__;
(2)利用所探索的结论,找一组正整数a、b、m、n填空:__+__![]() =(___)+__
=(___)+__![]() )2;
)2;
(3)若a+4![]() =
=![]() ,且a、m、n均为正整数,求a的值?
,且a、m、n均为正整数,求a的值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com