
 已知二次函数y=ax2+2ax+a-1(a>0).
已知二次函数y=ax2+2ax+a-1(a>0).分析 (1)只要证明△>0即可解决问题;
(2)利用顶点坐标公式计算即可;
(3)求出抛物线经过(1,2)和(1,6)时的a的值即可解决问题;
解答 (1)证明:∵△=(2a)2-4a(a-1)=4a,
∴a>0,
∴4a>0,
∴△>0,
∴抛物线与x轴有两个交点;
(2)∵-$\frac{2a}{2a}$=-1,$\frac{4a(a-1)-(2a)^{2}}{4a}$=-1,
∴抛物线的顶点坐标为(-1,-1);
(3)二次函数y=ax2+2ax+a-1经过(1,2)时,2=3a+a-1,解得a=$\frac{3}{4}$,
二次函数y=ax2+2ax+a-1经过(1,6)时,6=3a+a-1,解得a=$\frac{7}{4}$,
∴观察图象可知,函数值y的最小值范围是2≤y≤6,a的取值范围为$\frac{3}{4}$≤a≤$\frac{7}{4}$.
点评 本题考查二次函数由x轴的交点、二次函数的最值问题等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=4$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.
如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=4$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
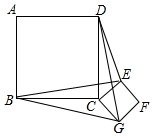 如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论是①②③(填序号)
如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论是①②③(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 | 9.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com