
【题目】如图①,在矩形 ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿 D→C→B→A路线运动,到A停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒bcm,点Q的速度变为每秒dcm.图②是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.
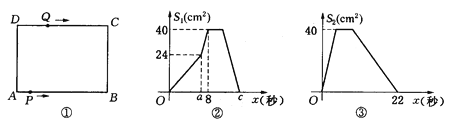
(1)、参照图象,求b、图②中c及d的值;
(2)、连接PQ,当PQ平分矩形ABCD的面积时,运动时间x的值为 ;
(3)、当两点改变速度后,设点P、Q在运动线路上相距的路程为y(cm),求y(cm)与运动时间x(秒)之间的函数关系式,并写出自变量x的取值范围;
(4)、若点P、点Q在运动路线上相距的路程为25cm,求x的值.
【答案】(1)、b=2;C=17;d=1;(2)、![]() ;(3)、当6<x≤
;(3)、当6<x≤![]() 时,y=28-3x; 当
时,y=28-3x; 当![]() <x≤17时,y=3x-28;当17<x≤22时,y=x+6;(4)、1秒或19秒.
<x≤17时,y=3x-28;当17<x≤22时,y=x+6;(4)、1秒或19秒.
【解析】
试题分析:(1)、首先根三角形面积求出a的值,然后得出b、c、d的值;(2)、平分面积则说明PQ经过四边形对角线的交点,然后根据性质求出x的值;(3)、利用待定系数法分6<x≤![]() ,
,![]() <x≤17和17<x≤22三种情况分别求出函数解析式;(4)、分别根据改变速度前和改变速度后两种情况列出一元一次方程,从而求出x的值.
<x≤17和17<x≤22三种情况分别求出函数解析式;(4)、分别根据改变速度前和改变速度后两种情况列出一元一次方程,从而求出x的值.
试题解析:(1)、观察图②得S△APD=![]() PAAD=
PAAD=![]() ×a×8=24, ∴a=6(秒),
×a×8=24, ∴a=6(秒),
![]() (厘米/秒),
(厘米/秒), ![]() (秒);
(秒);
(22﹣6)d=28﹣12, 解得d=1(厘米/秒);
(2)、![]()
(3)、当6<x≤![]() 时,y=28-3x 当
时,y=28-3x 当![]() <x≤17时,y=3x-28 当17<x≤22时,y=x+6
<x≤17时,y=3x-28 当17<x≤22时,y=x+6
(4)、改变速度前,28-3x=25,x=1 改变速度后,x+6=25,x=19
∴当点Q出发1或19秒时,点P、点Q在运动路线上相距的路程为25cm.


科目:初中数学 来源: 题型:
【题目】为了解某学校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况.并将所得数据进行了统计,结果如图所示.
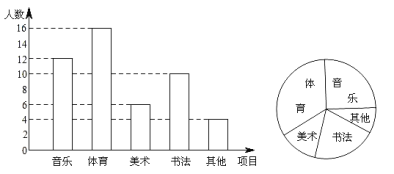
(1)求在这次调查中,一共抽查了多少名学生;
(2)求出扇形统计图中参加“音乐”活动项目所对扇形的圆心角的度数;
(3)若该校有2400名学生,请估计该校参加“美术”活动项目的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2016次操作后得到的折痕D2015E2015到BC的距离记为h2016,到BC的距离记为h2016.若h1=1,则h2016的值为( )
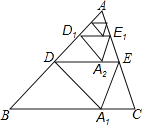
A.![]() B.1﹣
B.1﹣![]() C.
C.![]() D.2﹣
D.2﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,
∠BAD=45°,AD与BE交于点F,连接CF.
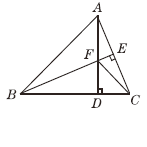
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
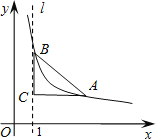
【题目】如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数![]() 的图象上.那么k的值是 .
的图象上.那么k的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】∠1与∠2是一组平行线被第三条直线所截的同旁内角,若∠1=50°,则( )
A. ∠2=50° B. ∠2=130° C. ∠2=50°或∠2=130° D. ∠2的大小不一定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com