
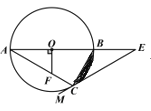
【题目】如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OF⊥AB,交AC于点F,点E在AB的延长线上,射线EM经过点C,且∠ACE+∠AFO=180°.
(1)求证:EM是⊙O的切线;
(2)若∠A=∠E,BC=![]() ,求阴影部分的面积.(结果保留
,求阴影部分的面积.(结果保留![]() 和根号).
和根号).
【答案】(1)详见解析;(2)![]() ;
;
【解析】
(1)连接OC,根据垂直的定义得到∠AOF=90°,根据三角形的内角和得到∠ACE=90°+∠A,根据等腰三角形的性质得到∠OCE=90°,得到OC⊥CE,于是得到结论;
(2)根据圆周角定理得到∠ACB=90°,推出∠ACO=∠BCE,得到△BOC是等边三角形,根据扇形和三角形的面积公式即可得到结论.
:(1)连接OC,
∵OF⊥AB,
∴∠AOF=90°,
∴∠A+∠AFO+90°=180°,
∵∠ACE+∠AFO=180°,
∴∠ACE=90°+∠A,
∵OA=OC,
∴∠A=∠ACO,
∴∠ACE=90°+∠ACO=∠ACO+∠OCE,
∴∠OCE=90°,
∴OC⊥CE,
∴EM是⊙O的切线;
(2)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACO+∠BCO=∠BCE+∠BCO=90°,
∴∠ACO=∠BCE,
∵∠A=∠E,
∴∠A=∠ACO=∠BCE=∠E,
∴∠ABC=∠BCO+∠E=2∠A,
∴∠A=30°,
∴∠BOC=60°,
∴△BOC是等边三角形,
∴OB=BC=![]() ,
,
∴阴影部分的面积=![]() ,
,


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:法国数学家韦达在研究一元二次方程时有一项重大发现:如果一元二次方程![]() 的两个根分别是
的两个根分别是![]() ,那么
,那么![]() ,
,![]() .
.
例如:已知方程![]() 的两根分别是
的两根分别是![]() ,
,
则:![]() ,
,![]() .
.
请同学们阅读后利用以上结论完成以下问题:
(1)已知方程![]() 的两根分别是
的两根分别是![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)已知方程![]() 的两根分别是
的两根分别是![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)若一元二次方程![]() 的一个根大于2,一个根小于2,求
的一个根大于2,一个根小于2,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晓琳和爸爸到太子河公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,晓琳继续前行5分钟后也原路返回,两人恰好同时到家.晓琳和爸爸在整个运动过程中离家的路程y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示,下列结论:①两人同行过程中的速度为200米/分;②m的值是15,n的值是3000;③晓琳开始返回时与爸爸相距1800米;④运动18分钟或30分钟时,两人相距900米.其中正确结论的个数是( )
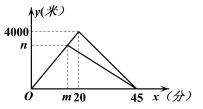
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省中小学积极开展综合实践活动,某校准备组织开展四项综合实践活动:“A.我是非遗小传人,B.学做家常餐,C.爱心义卖行动,D.找个岗位去体验”.为了解学生最喜爱哪项综合实践活动,随机抽取部分学生进行问卷调查(每位学生只能选择一项),将调查结果绘制成下面两幅不完整的统计图,请结合图中提供的信息回答下列问题:
(1)本次一共调查了 名学生,在扇形统计图中,m的值是 ;
(2)补全条形统计图;
(3)若该校共有1200名学生,估计最喜爱B和C项目的学生一共有多少名?
(4)现有最喜爱A,B,C,D活动项目的学生各一人,学校要从这四人中随机选取两人交流活动体会,请用列表或画树状图的方法求出恰好选取最喜爱C和D项目的两位学生的概率.
最喜爱各项综合实践活动条形统计图 最喜爱各项综合实践活动扇形统计图


查看答案和解析>>
科目:初中数学 来源: 题型:
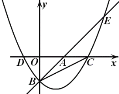
【题目】如图,直线y=x-3与坐标轴交于A、B两点,抛物线![]() 经过点B,与直线y=x-3交于点E(8,5),且与x轴交于C,D两点.
经过点B,与直线y=x-3交于点E(8,5),且与x轴交于C,D两点.
(1)求抛物线的解析式;
(2)抛物线上有一点M,当∠MBE=75°时,求点M的横坐标;
(3)点P在抛物线上,在坐标平面内是否存在点Q,使得以点P,Q,B,C为顶点的四边形是矩形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮从家出发步行到公交站台后,等公交车去学校,如图, 折线表示这个过程中行程 s (千米)与所花时间 t (分)之间的关系,下 列说法错误的是( )
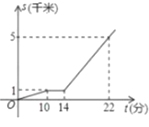
A.他家到公交车站台需行 1 千米B.他等公交车的时间为 4 分钟
C.公交车的速度是 500 米/分D.他步行与乘公交车行驶的平均速度300米/分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,两个完全相同的三角形纸片![]() 和
和![]() 重合放置,其中
重合放置,其中![]() ,
,![]() .
.
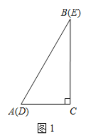
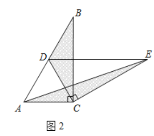

(1)操作发现:如图2,固定![]() ,使
,使![]() 绕点
绕点![]() 旋转,当点
旋转,当点![]() 恰好落在
恰好落在![]() 边上时,填空:①线段
边上时,填空:①线段![]() 与
与![]() 的位置关系是________;②设
的位置关系是________;②设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的数量关系是_____.
的数量关系是_____.
(2)猜想论证:当![]() 绕点
绕点![]() 旋转到如图3所示的位置时,请猜想(1)中
旋转到如图3所示的位置时,请猜想(1)中![]() 与
与![]() 的数量关系是否仍然成立?若成立,请证明;若不成立,请说明理由.
的数量关系是否仍然成立?若成立,请证明;若不成立,请说明理由.
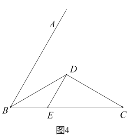
(3)拓展探究:已知![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() (如图4).若在射线
(如图4).若在射线![]() 上存在点
上存在点![]() ,使
,使![]() ,请求相应的
,请求相应的![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车租凭公司要购买轿车和面包车共![]() 辆,其中轿车最少要购买
辆,其中轿车最少要购买![]() 辆,轿车每辆
辆,轿车每辆![]() 万元,购头面包车每辆
万元,购头面包车每辆![]() 万元,公司可投入的购车资金不超过
万元,公司可投入的购车资金不超过![]() 万元.
万元.
(1)符合公司要求的购买方案有几种?请说明理由;
(2)如果每辆轿车日租金为![]() 元,每辆面包车日租金为
元,每辆面包车日租金为![]() 元,假设新购买的这
元,假设新购买的这![]() 辆汽车每日都可以全部租出,公司希望
辆汽车每日都可以全部租出,公司希望![]() 辆汽车的日租金最高,那么应该选择以上的哪种购买方案?且日租金最高为多少元?
辆汽车的日租金最高,那么应该选择以上的哪种购买方案?且日租金最高为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com