
【题目】某汽车租凭公司要购买轿车和面包车共![]() 辆,其中轿车最少要购买
辆,其中轿车最少要购买![]() 辆,轿车每辆
辆,轿车每辆![]() 万元,购头面包车每辆
万元,购头面包车每辆![]() 万元,公司可投入的购车资金不超过
万元,公司可投入的购车资金不超过![]() 万元.
万元.
(1)符合公司要求的购买方案有几种?请说明理由;
(2)如果每辆轿车日租金为![]() 元,每辆面包车日租金为
元,每辆面包车日租金为![]() 元,假设新购买的这
元,假设新购买的这![]() 辆汽车每日都可以全部租出,公司希望
辆汽车每日都可以全部租出,公司希望![]() 辆汽车的日租金最高,那么应该选择以上的哪种购买方案?且日租金最高为多少元?
辆汽车的日租金最高,那么应该选择以上的哪种购买方案?且日租金最高为多少元?
【答案】(1)三种,理由见解析;(2)购买5辆轿车,5辆面包车时,日租金最高为1550元.
【解析】
(1)本题首先根据题中的不等关系轿车最少要购买3辆及公司可投入的购车资金不超过55万元,列出不等式组,进而求出x的取值范围,即可确定符合公司要求的购买方案;
(2)本题先由题意求出日租金总额和轿车数量之间的函数关系,再根据一次函数的增减性求出使日租金最大的方案,进而得出具体的日租金.
解:(1)设购轿车x辆,
由已知得x≥3且7x+4(10-x)≤55,
∴解得3≤x≤5,
又因为x为正整数,
∴x=3、4、5,
∴符合题意的购买方案有三种;
(2)可设日租金总额为W,
则W=200x+110(10-x)=90x+1100.
∵90>0,
∴W随x的增大而增大,
∴x取5时,W最大=1550元,
∴可知购买5辆轿车,5辆面包车时,日租金最高为1550元.


科目:初中数学 来源: 题型:
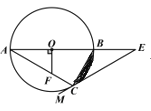
【题目】如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OF⊥AB,交AC于点F,点E在AB的延长线上,射线EM经过点C,且∠ACE+∠AFO=180°.
(1)求证:EM是⊙O的切线;
(2)若∠A=∠E,BC=![]() ,求阴影部分的面积.(结果保留
,求阴影部分的面积.(结果保留![]() 和根号).
和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,点P从点B出发,沿线段BA,向点A以
,点P从点B出发,沿线段BA,向点A以![]() 的速度匀速运动;点Q从点D出发,沿线段DC向点C以
的速度匀速运动;点Q从点D出发,沿线段DC向点C以![]() 的速度匀速运动,已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为
的速度匀速运动,已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为![]() .
.

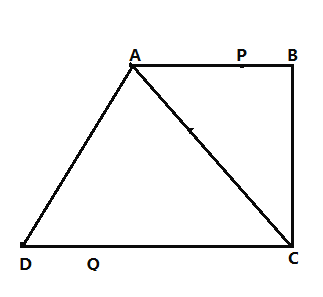
(1)连结P、Q两点,则线段PQ长的取值范围是________;
(2)当![]() cm时,求t的值;
cm时,求t的值;
(3)若在线段CD上有一点E,![]() cm,连结AC和PE.请问是否存在某一时刻使得AC平分PE?若存在,求出t的值;若不存在,请说明理由.
cm,连结AC和PE.请问是否存在某一时刻使得AC平分PE?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=2x2+bx+c与直线y=﹣1只有一个公共点,且经过A(m﹣1,n)和B(m+3,n),过点A,B分别作x轴的垂线,垂足记为M,N,则四边形AMNB的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家图文广告公司制作的宣传画板颇受商家欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.
画板的边长(dm) | 10 | 20 |
出售价(元/张) | 160 | 220 |
(1)求一张画板的出售价与边长之间满足的函数关系式;
(2)已知出售一张边长为30dm的画板,获得的利润为130元(利润=出售价-成本价),
①求一张画板的利润与边长之间满足的函数关系式;
②当边长为多少时,出售一张画板所获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() .
.
(1)如果该方程有两个不相等的实数根,求m的取值范围;
(2)在(1)的条件下,当关于x的抛物线![]() 与x轴交点的横坐标都是整数,且
与x轴交点的横坐标都是整数,且![]() 时,求m的整数值.
时,求m的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,AB=6,AD=8,将矩形ABCD绕点A顺时针旋转θ(0°<θ<360°)得到矩形AEFG,当θ=_____°时,GC=GB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边(
表示直角三角形的两直角边(![]() ),下列四个说法:
),下列四个说法:

①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
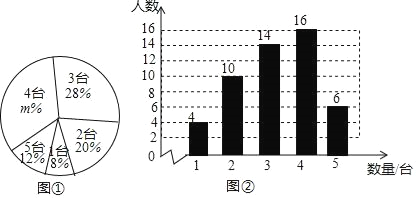
【题目】随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(2)求本次调查获取的样本数据的众数、中位数和平均数;
(3)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com