
【题目】一家图文广告公司制作的宣传画板颇受商家欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.
画板的边长(dm) | 10 | 20 |
出售价(元/张) | 160 | 220 |
(1)求一张画板的出售价与边长之间满足的函数关系式;
(2)已知出售一张边长为30dm的画板,获得的利润为130元(利润=出售价-成本价),
①求一张画板的利润与边长之间满足的函数关系式;
②当边长为多少时,出售一张画板所获得的利润最大?最大利润是多少?
【答案】(1)满足函数关系式y=6x+100;(2)①W=-![]() x2+6x+100;②正方形画板的边长为18dm时,可获最大利润154元.
x2+6x+100;②正方形画板的边长为18dm时,可获最大利润154元.
【解析】
试题(1)每张画板的成本价与它的面积成正比例,可设其解析式为y成本价=ax2,每张画板的出售价由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.可设y出售价=kx+b.把表中数据代入即可求出结论;
(2)由y利润=y出售价-y成本价,可得出二次函数,求出其最大值即可.
试题解析:(1)设正方形画板的边长为xdm,出售价为每张y元,且y=kx+b(k≠0) (1分)
由表格中的数据可得,![]() ,解得
,解得![]()
从而一张画板的出售价y与边长x之间满足函数关系式y=6x+100
(2)设每张画板的成本价为ax2,利润W=6x+100-ax2
当x=30时,W=130,180+100-900a=130,得a=![]()
一张画板的利润W与边长x之间满足函数关系式W=-![]() x2+6x+100
x2+6x+100
由W=-16(x-18)2+154,知当x=18时,W有最大值,W最大=154
因此当正方形画板的边长为18dm时,可获最大利润154元.
考点: 1.一次函数表达式;2.二次函数表达式;3.二次函数的最大值.


科目:初中数学 来源: 题型:
【题目】(1)如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;
(2)如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程.
(3)若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?
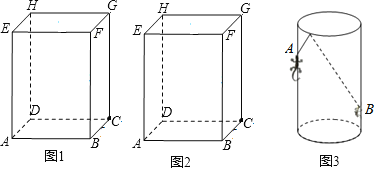
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (k为常数,k≠1).
(k为常数,k≠1).
(1)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(2)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(3)若其图象的一支位于第二象限,在这一支上任取两点A(x1、x2)、B(x2、y2),当y1>y2时,试比较x1与x2的大小;
(4)若在其图象上任取一点,向x轴和y轴作垂线,若所得矩形面积为6,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,∠B=60°,点E,F分别是BC,CD上的两个动点,且始终保持∠AEF=60°.
(1)试判断△AEF的形状并说明理由;
(2)若菱形的边长为2,求△ECF周长的最小值.
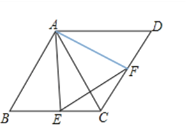
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0,其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数![]() (a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为
(a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为![]() ,直线l的解析式为y=x.
,直线l的解析式为y=x.
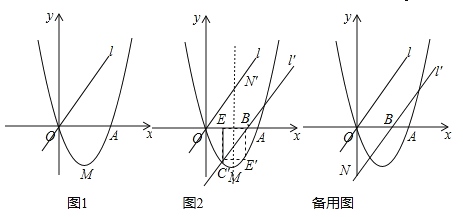
(1)求二次函数的解析式;
(2)直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E恰好落在抛物线上点E′时(图2),求直线l′的解析式;
(3)在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E为AB的中点,F为BC上任意一点,把△BEF沿直线EF翻折,点B的对应点B′落在对角线AC上,则与∠FEB一定相等的角(不含∠FEB)有( )
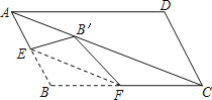
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在点B处,直角顶点F在CD的延长线上,BF与AD交于点G,斜边与CD交于点E![]() ,若CE=1,则DG的长为( )
,若CE=1,则DG的长为( )
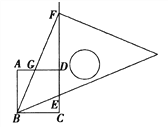
A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,H、F分别为AD、BC边的中点,四边形EFGH为矩形,E、G分别在AB、CD边上,则图中四个直角三角形面积之和与矩形EFGH的面积之比为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com