
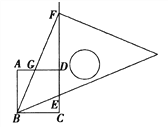
【题目】如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在点B处,直角顶点F在CD的延长线上,BF与AD交于点G,斜边与CD交于点E![]() ,若CE=1,则DG的长为( )
,若CE=1,则DG的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,求DE与BC的数量关系;
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,∠PDF=60°连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在正方形ABCD中,E为CD边上的一点,F为BC的延长线上一点,CE=CF。
⑴△BCE与△DCF全等吗?说明理由;
⑵若∠BEC=60o,求∠EFD。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个Rt△DEF直角边DE落在AB上,过A点作射线AC与斜边EF平行,已知AB=12,DE=4,DF=3,点P从A点出发,沿射线AC方向以每秒2个单位的速度运动,Q为AP中点,设运动时间为t秒(t>0) 
(1)若点D与点B重合,当t=5时,连接QE,PF,此时△AQE为三角形、四边形QEFP为形;
(2)如图②,若在点P运动时,Rt△DEF同时沿着BA方向以每秒1个单位的速度运动,当D点到A点时,两个运动都停止. ①如图①,若M为EF中点,当D、M、Q三点在同一直线上时,求t的值;
②在运动过程中,以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切时,求运动时间t.
查看答案和解析>>
科目:初中数学 来源: 题型:
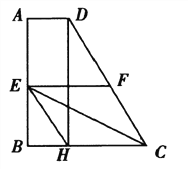
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=6,CD=8,E,F分别是边ABCD的中点, DH⊥BC于点H,连接EH,EC,EF,现有下列结论:①∠CDH=30°;②EF=4;③四边形EFCH是菱形;④S△EFC=3S△BEH.你认为结论正确的有___________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)计算:(π﹣ ![]() )0+
)0+ ![]() +(﹣1)2013﹣
+(﹣1)2013﹣ ![]() tan60°;
tan60°;
(2)先化简,再求值:(a+3)2+a(4﹣a),其中a为(1)中计算的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=![]() ,求ED的长.
,求ED的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用若干个大小相同,棱长为1的小正方体搭成一个几何体模型,其三视图如图所示,则搭成这个几何体模型所用的小正方体的个数是( )

A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com