
【题目】如图,一个Rt△DEF直角边DE落在AB上,过A点作射线AC与斜边EF平行,已知AB=12,DE=4,DF=3,点P从A点出发,沿射线AC方向以每秒2个单位的速度运动,Q为AP中点,设运动时间为t秒(t>0) 
(1)若点D与点B重合,当t=5时,连接QE,PF,此时△AQE为三角形、四边形QEFP为形;
(2)如图②,若在点P运动时,Rt△DEF同时沿着BA方向以每秒1个单位的速度运动,当D点到A点时,两个运动都停止. ①如图①,若M为EF中点,当D、M、Q三点在同一直线上时,求t的值;
②在运动过程中,以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切时,求运动时间t.
【答案】
(1)等腰;菱
(2)解:①当D、M、Q三点在同一直线上时,如图②,
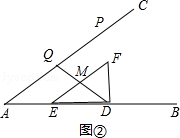
此时AQ=t,EM= ![]() EF=
EF= ![]() ,AD=12﹣t,DE=4.
,AD=12﹣t,DE=4.
∵EF∥AC,
∴△DEM∽△DAQ,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得t= ![]() ;
;
②存在以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切,
此时点Q在∠ADF的角平分线上或在∠FDB的角平分线上.
Ⅰ.当点Q在∠ADF的角平分线上时,
过点Q作QH⊥AB于H,如图③,
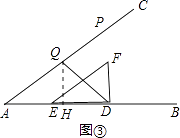
则有∠HQD=∠HDQ=45°,
∴QH=DH.
∵△AHQ∽△EDF(已证),
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴QH= ![]() ,AH=
,AH= ![]() ,
,
∴DH=QH= ![]() .
.
∵AB=AH+HD+BD=12,DB=t,
∴ ![]() +
+ ![]() +t=12,
+t=12,
∴t=5;
Ⅱ.当点Q在∠FDB的角平分线上时,
过点Q作QH⊥AB于H,如图④,
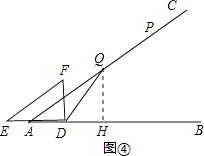
同理可得DH=QH= ![]() ,AH=
,AH= ![]() .
.
∵AB=AD+DB=AH﹣DH+DB=12,DB=t,
∴ ![]() ﹣
﹣ ![]() +t=12,
+t=12,
∴t=10.
综上所述:当t为5秒或10秒时,以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切.
【解析】解:(1)四边形EFPQ是菱形. 理由:过点Q作QH⊥AB于H,如图①,
∵t=5,∴AP=2×5=10.
∵点Q是AP的中点,
∴AQ=PQ=5.
∵∠EDF=90°,DE=4,DF=3,
∴EF= ![]() =5,
=5,
∴PQ=EF=5.
∵AC∥EF,
∴四边形EFPQ是平行四边形,且∠A=∠FEB.
又∵∠QHA=∠FDE=90°,
∴△AHQ∽△EDF,
∴ ![]() =
= ![]() =
= ![]() .
.
∵AQ=EF=5,
∴AH=ED=4.
∵AE=12﹣4=8,
∴HE=8﹣4=4,
∴AH=EH,
∴AQ=EQ,
∴PQ=EQ,
∴△AQE是等腰三角形,平行四边形EFPQ是菱形;
所以答案是:等腰,菱形.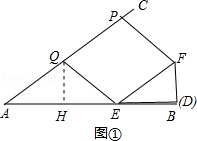


科目:初中数学 来源: 题型:
【题目】如图所示的格点纸中每个小正方形的边长均为1,以小正方形的顶点为圆心,2为半径做了一个扇形,用该扇形围成一个圆锥的侧面,针对此做法,小明和小亮通过计算得出以下结论:小明说此圆锥的侧面积为 ![]() π;小亮说此圆锥的弧长为
π;小亮说此圆锥的弧长为 ![]() π,则下列结论正确的是( )
π,则下列结论正确的是( ) 
A.只有小明对
B.只有小亮对
C.两人都对
D.两人都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,对两人进行了五次模拟,并对成绩(单位:分)进行了整理,计算出 ![]() =83分,
=83分, ![]() =82分,绘制成如下尚不完整的统计图表. 甲、乙两人模拟成绩统计表
=82分,绘制成如下尚不完整的统计图表. 甲、乙两人模拟成绩统计表
① | ② | ③ | ④ | ⑤ | |
甲成绩/分 | 79 | 86 | 82 | a | 83 |
乙成绩/分 | 88 | 79 | 90 | 81 | 72 |
根据以上信息,回答下列问题:
(1)a=
(2)请完成图中表示甲成绩变化情况的折线. 
(3)经计算S甲2=6,S乙2=42,综合分析,你认为选拔谁参加比赛更合适,说明理由.
(4)如果分别从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于82分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF 与AB、CD的延长线分别
交于E、F.
(1)证明:△BOE≌△DOF.
(2)当EF与AC满足什么条件时,四边形AECF是菱形,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在点B处,直角顶点F在CD的延长线上,BF与AD交于点G,斜边与CD交于点E![]() ,若CE=1,则DG的长为( )
,若CE=1,则DG的长为( )
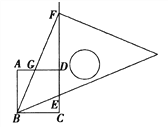
A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
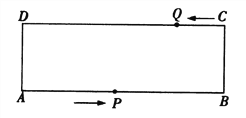
【题目】如图,在矩形ABCD中,AB=24 cm, BC=8 cm,点P从点A开始沿折线A-B-C-D以4 cm/s的速度移动,点Q从点C开始沿CD边以2 cm/s的速度移动,如果点P,Q分别从点A,C同时出发,当其中一点到达点D时,另一点也随之停止运动,设运动时间为ts.当t为何值时,四边形QPBC为矩形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读)|4﹣1|表示4与1差的绝对值,也可以理解为4与1两数在数轴上所对应的两点之间的距离;|4+1|可以看做|4﹣(﹣1)|,表示4与﹣1的差的绝对值,也可以理解为4与﹣1两数在数轴上所对应的两点间的距离.
(1)|4﹣(﹣1)|=
(2)|5+2|=
![]()
(3)利用数轴找出所有符合条件的整数x,使得|x+3|=5,则x= .
(4)利用数轴找出所有符合条件的整数x,使得|x+3|+|x﹣2|=5,这样的整数是: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,然后解答问题.
探究:用的幂的形式表示aman的结果(m、为正整数).
根据乘方的意义,aman=![]() =am+n.
=am+n.
(1)请根据以上结论填空:36×38= ,52×53×57= ,(a+b)3(a+b)5= ;
(2)仿照以上的分析过程,用的幂的形式表示(am)n的结果(提示:将am看成一个整体).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com