
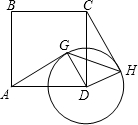
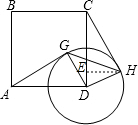
 如图,在边长为4的正方形ABCD中,以D为圆心、2为半径画圆,点G是⊙D上任意一点,连接GD、AG.将GD绕点D按顺时针方向旋转90°,得到DH,连接CH、GH.
如图,在边长为4的正方形ABCD中,以D为圆心、2为半径画圆,点G是⊙D上任意一点,连接GD、AG.将GD绕点D按顺时针方向旋转90°,得到DH,连接CH、GH.| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
|
| CD2-DH2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
2×2
| ||
| 4 |
| 3 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
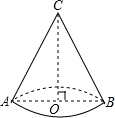 亮亮同学为了参加兰州市第十届中小学生艺术节,用纸板制作了一个圆锥形纸帽,如图所示,它的底面半径0B=9,高0C=12. 若不计损耗,则这个圆锥形纸帽的侧面积是
亮亮同学为了参加兰州市第十届中小学生艺术节,用纸板制作了一个圆锥形纸帽,如图所示,它的底面半径0B=9,高0C=12. 若不计损耗,则这个圆锥形纸帽的侧面积是| A、90π | B、120π |
| C、135π | D、150π |
查看答案和解析>>
科目:初中数学 来源: 题型:
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com