
【题目】已知函数y1=![]() x+2的图象分别与坐标轴相交于A,B两点(如图所示),与反比例函数y2=
x+2的图象分别与坐标轴相交于A,B两点(如图所示),与反比例函数y2=![]() (x>0)的图象相交于C点.
(x>0)的图象相交于C点.
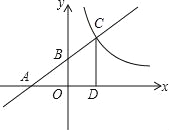
(1)写出A、B两点的坐标;
(2)作CD⊥x轴,垂足为D,如果OB是△ACD的中位线,求反比例函数y=![]() (x>0)的关系式;
(x>0)的关系式;
(3)根据图象(x>0)直接写出y1>y2时的取值范围.
【答案】(1)B(0,2),A(﹣3,0)(2)![]() (3)x>3
(3)x>3
【解析】
试题分析:(1)分别令一次函数解析式中x=0、y=0求出y、x的值,从而得出点A、B的坐标;
(2)由A、B点的坐标结合中位线的性质,找出线段OD、DC的长度,从而找出点C的坐标,再由点C的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数的系数k,从而得出结论;
(3)观察函数图象,根据两函数图象的上下关系结合交点的坐标,即可得出结论.
试题解析:(1)令一次函数y1=![]() x+2中x=0,则y=2,
x+2中x=0,则y=2,
∴点B的坐标为(0,2);
令一次函数y1=![]() x+2中y=0,则
x+2中y=0,则![]() x+2=0,
x+2=0,
解得:x=﹣3,
∴点A的坐标为(﹣3,0).
(2)∵OB是△ACD的中位线,
∴![]() ,
,
∵点A(﹣3,0),点B(0,2),
∴AD=6,DC=4,OD=AD﹣AO=6﹣3=3,
∴点C的坐标为(3,4).
又∵点C在反比例函数y2=![]() (x>0)的图象上,
(x>0)的图象上,
∴k=3×4=12,
∴反比例函数解析式为y2=![]() (x>0).
(x>0).
(3)观察函数图象,发现:
当x>3时,一次函数图象在反比例函数图象的上方,
∴不等式y1>y2时的取值范围为x>3.


 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】下列三个命题:①圆既是轴对称图形又是中心对称图形;②垂直于弦的直径平分弦;③ 相等的圆心角所对的弧相等.④在同圆或等圆中,如果两条弧相等,那么弦也相等。其中真命题的是( )
A. ①②
B. ②④
C. ①②④
D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆一中综合实践活动艺体课程组为了解学生最喜欢的球类运动,对足球、乒乓球、篮球、排球四个项目进行了调查,并将调查的结果绘制成如下的两幅统计图(说明:每位同学只选一种自己最喜欢的球类),请你根据图中提供的信息解答下列问题:
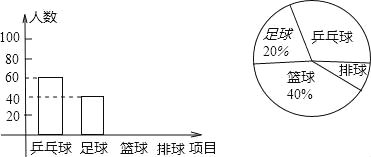
(1)求这次接受调查的学生人数,并补全条形统计图;
(2)求扇形统计图中喜欢排球的圆心角度数;
(3)若调查到爱好“乒乓球”的5名学生中有3名男生,2名女生,现从这5名学生中任意抽取2名学生,请用列表法或画树状图的方法,求出刚好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在矩形ABCD中,AB=a,BC=b,动点M从点A出发沿边AD向点D运动.
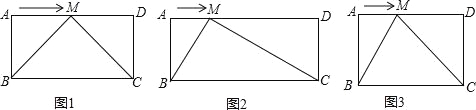
(1)如图1,当b=2a,点M运动到边AD的中点时,请证明∠BMC=90°;
(2)如图2,当b>2a时,点M在运动的过程中,是否存在∠BMC=90°,若存在,请给与证明;若不存在,请说明理由;
(3)如图3,当b<2a时,(2)中的结论是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆客房部有60个房间供旅客居住,当每个房间的定价为每天200元时,房间可以住满。每个房间每天的定价每提高10元,就会有一个房间空闲,对有游客人住的房间,宾馆需对每个房间每天支出20元的各种费用;设每个房间每天的定价增加x元,则
(1)房间每天的入住间数__________间(用x的代数式表示);
(2)该宾馆每天的房间所收费用为_________元(用x的代数式表示);
(3)若该宾馆客房部希望每天的利润为14000元,则每个房间的定价应为每天多少元?
(为了吸引游客,每个房间的定价不会高于500元)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种植基地 2017 年蔬菜产量为 100 吨,预计 2019 年蔬菜产量将达到 144吨,据此估计该种植基地蔬菜产量的年平均增长率(百分数)为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个相似多边形的一组对应边分别为3cm和4.5cm,如果它们的面积和为78cm2,那么较大多边形的面积为( )
A. 46.8 cm2 B. 42 cm2 C. 52 cm2 D. 54 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com