
【题目】如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E. 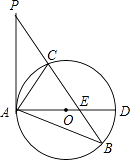
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点C,若ACAB=12,求AC的长.
【答案】
(1)证明:连接CD,如图,
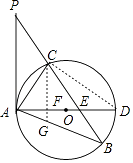
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠CAD+∠D=90°,
∵∠PAC=∠PBA,
∠D=∠PBA,
∴∠CAD+∠PAC=90°,即∠PAD=90°,
∴PA⊥AD,
∴PA是⊙O的切线
(2)解:∵CF⊥AD,
∴∠ACF+∠CAF=90°,∠CAD+∠D=90°,
∴∠ACF=∠D,
∴∠ACF=∠B,
而∠CAG=∠BAC,
∴△ACG∽△ABC,
∴AC:AB=AG:AC,
∴AC2=AGAB=12,
∴AC=2 ![]()
【解析】(1)连接CD,如图,利用圆周角定理得到∠CAD+∠D=90°,再∠D=∠PBA,加上∠PAC=∠PBA,所以∠PAD=90°,然后根据切线的判定定理即可得到结论;(2)证明△ACG∽△ABC,再利用相似比得到AC2=AGAB=12,从而得到AC=2 ![]() .
.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图①,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
(1)如图②,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图③,点B、C分别在∠MAN的边AM、AN上,点E、F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE与△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.
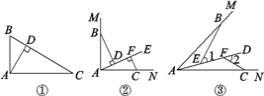
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在Rt△ABC和Rt△A'B'C'中,AB=A'B',AC=A'C',C=∠C'=90°.
求证:Rt△ABC和Rt△A'B'C'全等.
(1)请你用“如果…,那么…”的形式叙述上述命题;
(2)将△ABC和△A'B'C'拼在一起,请你画出两种拼接图形;例如图2:(即使点A与点A'重合,点C与点C'重合.)
(3)请你选择你拼成的其中一种图形,证明该命题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点. 
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使得点A落在点A'处,当A'E⊥AC时,A'B= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
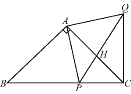
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,点P是BC上的一动点,AP=AQ,∠PAQ=90°,连接CQ.
(1)求证:CQ⊥BC.
(2)△ACQ能否是直角三角形?若能,请直接写出此时点P的位置;若不能,请说明理由.
(3)当点P在BC上什么位置时,△ACQ是等腰三角形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com