
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先变形得到原式=4$\sqrt{3}$-$\frac{3\sqrt{6}}{2}$+$\sqrt{3}$($\sqrt{3}$-1)•$\frac{1}{\sqrt{3}}$($\sqrt{3}$+1),然后利用平方差公式计算;
(3)利用二次根式的乘除法则和平方差公式计算.
解答 解:(1)原式=4$\sqrt{3}$+2$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$-$\frac{8\sqrt{3}}{3}$
=2$\sqrt{3}$;
(2)原式=4$\sqrt{3}$-$\frac{3\sqrt{6}}{2}$+$\sqrt{3}$($\sqrt{3}$-1)•$\frac{1}{\sqrt{3}}$($\sqrt{3}$+1)
=4$\sqrt{3}$-$\frac{3\sqrt{6}}{2}$+2;
(3)原式=4$\sqrt{3}$-2$\sqrt{2}$+2$\sqrt{2}$×$\sqrt{3}$-(27-20)
=4$\sqrt{3}$-2$\sqrt{2}$+2$\sqrt{6}$-7.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC=10,BC=10$\sqrt{3}$.
如图,在△ABC中,AB=AC=10,BC=10$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
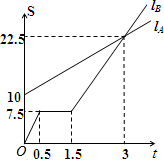 如图,LA,LB分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系.根据图象,回答下列问题:
如图,LA,LB分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系.根据图象,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=2,则两平行线AD与BC间的距离为( )
如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=2,则两平行线AD与BC间的距离为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com