
����Ŀ����ͼ���ھ���ABCD�У�AB��6��BC��8������P�ӵ�A������AC���յ�C�˶���ͬʱ����Q�ӵ�B������BA���A�˶�������A��ʱֹͣ�˶�����PҲͬʱֹͣ����P��Q�˶��ٶȾ�Ϊÿ��1����λ���ȣ�����PQ�����˶�ʱ��Ϊt(t��0)�룮
(1)����Q��B����A���˶�ʱ(δ����A��)��
�ٵ�t��_____ʱPQ��BC
�����APQ�����S����t�ĺ�����ϵʽ����д��t��ȡֵ��Χ��
(2)������P��Q������˶����߶�PQ�Ĵ�ֱƽ����Ϊl��
�ٵ�l������Aʱ������QP��AD�ڵ�E�����ʱ��t��ֵ��AE�ij���
�ڵ�l������Bʱ����t��ֵ��

���𰸡�(1)��![]() �룻��S��APQ����
�룻��S��APQ����![]() +
+![]() t(0��t��6)��(2)��t��3��AE��6����t��5��
t(0��t��6)��(2)��t��3��AE��6����t��5��
��������
(1)����ΪPQ��BC������ƽ���߷��߶γɱ������ɵ�![]() ���ҵ�����t�ķ��̣���⼴�ɣ��ڹ�P��PE��AB��E�����á�BAC�����ң��������PE�ij�������ҵ�S��t�ĺ�����ϵʽ��
���ҵ�����t�ķ��̣���⼴�ɣ��ڹ�P��PE��AB��E�����á�BAC�����ң��������PE�ij�������ҵ�S��t�ĺ�����ϵʽ��
(2)����ΪlΪPQ�Ĵ�ֱƽ�����ҹ���A������AP=AQ���ɴ˿������t��ֵ���ӳ�QP��CD��M�����õ���APQ�͡�CPM���ƣ��ҵ����Ʊȿ����AE�ij����ڵ�l����Bʱ���ɵ�BQ=BP=AP����P��PG��AB��G���������ߺ�һ�ɵ�AG=BG������PG��BC����ת����PҲΪAC���е㣬���������AP��ֵ�������ҵ�t��ֵ.
�⣺(1)��������ã�BQ��AP��t��
���ı���ABCD�Ǿ��Σ�
���ABC��90����
��AB��6��BC��8��
��AC��10��AQ��6��t��
��PQ��BC��
��![]() ��
��
��![]() ��
��
t��![]() ��
��
��t��![]() ��ʱ��PQ��BC��
��ʱ��PQ��BC��
�ʴ�Ϊ��![]() �룻
�룻
����ͼ1����P��PE��AB��E��
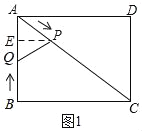
sin��BAC��![]() ��
��
��![]() ��PE��
��PE��![]() t��
t��
��S��APQ��![]() AQPE��
AQPE��![]() (6��t)
(6��t)![]()
![]() t����
t����![]() +
+![]() t(0��t��6)��
t(0��t��6)��
(2)����ͼ2���ӳ�CD��QP��M��
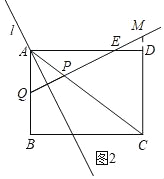
���߶�PQ�Ĵ�ֱƽ����Ϊl������A��
��AQ��AP����6��t��t��
��t��3��
��AQ��AP��3��CP��10��3��7��
��AQ��CD��
���AQP�ס�CMP��
��![]() ��
��
��![]()
![]() ��CM��7��
��CM��7��
��DM��7��6��1��
��AQ��DM��
���AQE�ס�DME��
��![]() ��
��![]() ��
��
��AE+DE��8��
��AE��6��
����ͼ3������PB����P��PG��AB��G����PG��BC��
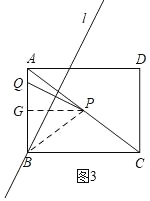
���߶�PQ�Ĵ�ֱƽ����l������B��
��PB��BQ��t��AP��
��AG��BG��
��AP��PC��![]() AC��5��
AC��5��
��t��5��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
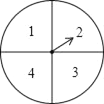
����Ŀ����ͼ����һ����������ת����ת�̱�ƽ���ֳ�4�����Σ��ֱ����1��2��3��4�ĸ����֣�С����С���ת��һ��ת��Ϊһ����Ϸ����ÿ��ת��ֹͣ��ָ����ָ�����ڵ���Ϊ�������õ�����һ����Ϸ�����õ�һ��������ָ��ָ�ڷֽ���ʱ��ת������1����������״ͼ���б��ķ�����ʾ��ÿ����Ϸ���ܳ��ֵ����н������2����ÿ����Ϸ�����õ���һ����ǡ���Ƿ���x2��4x+3��0�Ľ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧ��������㷨�����κ���y��ax2+bx+c��a��0����ͼ��ʱ����ȡ�Ա���x��һЩֵ���������Ӧ�ĺ���ֵy�����±���ʾ��
x | �� | 0 | 1 | 2 | 3 | 4 | �� |
y | �� | ��3 | 0 | ��1 | 0 | ��3 | �� |
���ţ��������ʱ���֣���������һ�����ݼ����������������һ�������ǣ�������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
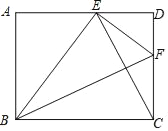
����Ŀ����ͼ���ھ���ABCD�У���E�DZ�AD�ϵĵ㣬EF��BE������CD�ڵ�F������CE��BF�����tan��ABE��![]() ����ôCE��BF��_____��
����ôCE��BF��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
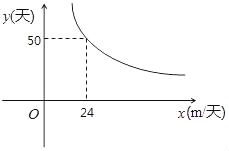
����Ŀ���ڹ���ʵʩ�����У�ij���̶ӽ���һ���ˮ���Ĺ��̣���������y(��)��ÿ����ɹ�����x�ĺ�����ϵͼ����ͼ��ʾ����˫���ߵ�һ���֣�
(1)��������⣬��y��x֮��ĺ�������ʽ��
(2)���ù��̶���2̨�ھ����ÿ̨�ھ��ÿ���ܹ�����ˮ��30�ף��ʸù��̶���Ҫ�ö����������ɴ�������
(3)���Ϊ�˷�Ѵ�����Ľ�����Ҫ��������10�������������ôÿ������Ҫ��ɶ����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ŀڴ���װ���ĸ��ֱ����1��2��3��4��С�����ǵ���״����С����ȫ��ͬ��С���ȴӿڴ���������Żص�ȡ��һ��С��������Ϊx��С����ʣ��������С�������ȡ��һ��С��������y��
��1��������x��yȷ���ĵ㣨x��y���ں���y=��x+6ͼ���ϵĸ��ʣ�
��2��С����С��Լ����һ����Ϸ��������ǣ���x��y����xy��6����С��ʤ����x��y����xy��6����С��ʤ�������Ϸ����ƽ��˵�����ɣ�������ƽ����������Ϸ����Ŷ�˫����ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AC��BD�ཻ�ڵ�O����E��OA���е㣬����BE���ӳ���AD�ڵ�F����֪S��AEF=4�������н��ۣ���![]() ����S��BCE=36����S��ABE=12���ܡ�AEF����ACD������һ����ȷ���ǣ�������
����S��BCE=36����S��ABE=12���ܡ�AEF����ACD������һ����ȷ���ǣ�������

A. �٢ڢۢ� B. �٢� C. �ڢۢ� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AC��BD�ཻ�ڵ�O����E��OA���е㣬����BE���ӳ���AD�ڵ�F����֪S��AEF=4�������н��ۣ���![]() ����S��BCE=36����S��ABE=12���ܡ�AEF����ACD������һ����ȷ���ǣ�������
����S��BCE=36����S��ABE=12���ܡ�AEF����ACD������һ����ȷ���ǣ�������

A. �٢ڢۢ� B. �٢� C. �ڢۢ� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ABC�У���BC��Ϊ12����AD��Ϊ8
��1����ͼ������EFGH�ı�GH��BC���ϣ�������������E��F�ֱ���AB��AC���ϣ�EF��AD�ڵ�K
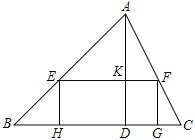
����![]() ��ֵ
��ֵ
����EH=x������EFGH�����ΪS����S��x�ĺ�����ϵʽ������S�����ֵ
��2����ABAC��������PQMN��������������ABCһ���ϣ�����������ֱ�����ABC���������ϣ�ֱ��д��������PQMN�ı߳���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com