
【题目】如图1,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A、C分别在x轴、y轴的正半轴上,且OA=2,OC=1,矩形对角线AC、OB相交于E,过点E的直线与边OA、BC分别相交于点G、H. 
(1)直接写出点E的坐标: .
(2)求证:AG=CH.
(3)如图2,以O为圆心,OC为半径的圆弧交OA与D,若直线GH与弧CD所在的圆相切于矩形内一点F,求直线GH的函数关系式. 
(4)在(3)的结论下,梯形ABHG的内部有一点P,当⊙P与HG、GA、AB都相切时,求⊙P的半径.
【答案】
(1)(1, ![]() )
)
(2)解:证明:∵矩形OABC,
∴CE=AE,BC∥OA,
∴∠HCE=∠EAG,
∵在△CHE和△AGE中
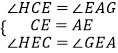 ,
,
∴△CHE≌△AGE,
∴AG=CH
(3)解:解:如图2,连接DE并延长DE交CB于M,连接AC,
∵DO=OC=1= ![]() OA,
OA,
∴D是OA的中点,
∵BC∥OA,
∴∠MCE=∠DAE,
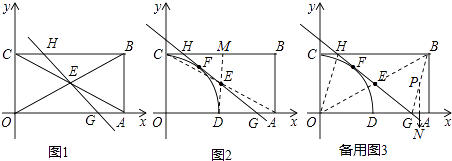
∵在△CME和△ADE中
 ,
,
∴△CME≌△ADE,
∴CM=AD=2﹣1=1,
∵四边形OABC是矩形,
∴∠MCO=∠COD=90°,CB∥OA,
∵OD=1,OA=2,
∴OD=AD,
∵矩形OABC的对角线交于E,
∴E为中心,
∴DE∥OC,
∴四边形CMDO是矩形,
∴MD⊥OD,MD⊥CB,
∴MD切⊙O于D,
∵HG切⊙O于F,E(1, ![]() ),
),
∴可设CH=HF=x,FE=ED= ![]() MD,
MD, 
在Rt△MHE中,有MH2+ME2=HE2,
即(1﹣x)2+( ![]() )2=(
)2=( ![]() +x)2,
+x)2,
解得x= ![]() ,
,
∴H( ![]() ,1),OG=2﹣
,1),OG=2﹣ ![]() =
= ![]() ,
,
∴G( ![]() ,0),
,0),
设直线GH的解析式是:y=kx+b,
把G、H的坐标代入得: ![]() k+b=0,且1=
k+b=0,且1= ![]() k+b,
k+b,
解得:k=﹣ ![]() ,b=
,b= ![]() ,
,
∴直线GH的函数关系式为y=﹣ ![]() x+
x+ ![]()
(4)解:解:如备用图3,连接BG,过P做PN⊥GA,垂足为N,
∵在△OCH和△BAG中
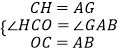 ,
,
∴△OCH≌△BAG,
∴∠CHO=∠AGB,
∵∠HCO=90°,
∴HC切⊙O于C,HG切⊙O于F,
∴OH平分∠CHF,
∴∠CHO=∠FHO=∠BGA,
∵四边形OCBA是矩形,
∴BC∥OA,BC=OA,
∵CH=AG(已证),
∴BH=OG,BH∥OG,
∴四边形BHOG是平行四边形,
∴OH∥BG,
∴∠OHE=∠BGE,
∵∠CHO=∠FHO=∠BGA
∴∠BGA=∠BGE,
即BG平分∠FGA,
∵⊙P与HG、GA、AB都相切,
∴和∠HGA的两边都相切的圆的圆心在∠HGA的角平分线上,即在GB上
∴圆心P必在BG上,
∴△GPN∽△GBA,
∴ ![]() ,
,
设半径为r,
![]() =
= ![]() ,
,
解得:r= ![]() .
.
答:⊙P的半径是 ![]()
【解析】(1)解:E的坐标是:(1, ![]() ), 所以答案是:(1,
), 所以答案是:(1, ![]() );
);
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.


 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( ) 
A.垂线段最短
B.经过一点有无数条直线
C.经过两点,有且仅有一条直线
D.两点之间,线段最短
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饮料厂以300千克的A种果汁和240千克的B种果汁为原料,配制生产甲、乙两种新型饮料,已知每千克甲种饮料含0.6千克A种果汁,含0.3千克B种果汁;每千克乙种饮料含0.2千克A种果汁,含0.4千克B种果汁.饮料厂计划生产甲、乙两种新型饮料共650千克,设该厂生产甲种饮料x(千克).
(1)列出满足题意的关于x的不等式组,并求出x的取值范围;
(2)已知该饮料厂的甲种饮料销售价是每1千克3元,乙种饮料销售价是每1千克4元,那么该饮料厂生产甲、乙两种饮料各多少千克,才能使得这批饮料销售总金额最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣3x+2和一次函数y=﹣2x+4,把y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.现有点A(2,0)和抛物线E上的点B(﹣1,n),请完成下列任务:
(1)当t=2时,抛物线E的顶点坐标是;
(2)判断点A是否在抛物线E上;
(3)求n的值.
(4)通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线E总过定点,这个定点的坐标是 .
(5)二次函数y=﹣3x2+5x+2是二次函数y=x2﹣3x+2和一次函数y=﹣2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
(6)以AB为一边作矩形ABCD,使得其中一个顶点落在y轴上,若抛物线E经过点A、B、C、D中的三点,求出所有符合条件的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扬州市中小学全面开展“体艺2+1”活动,某校根据学校实际,决定开设A:篮球,B:乒乓球,C:声乐,D:健美操等四中活动项目,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制了两幅不完整的统计图.请回答下列问题: 
(1)这次被调查的学生共有人.
(2)请你将统计图1补充完整.
(3)统计图2中D项目对应的扇形的圆心角是度.
(4)已知该校学生2400人,请根据调查结果估计该校最喜欢乒乓球的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第三十届夏季奥林匹克运动会将于2012年7月27日至8月12日在英国伦敦举行,目前正在进行火炬传递活动.某校学生会为了确定近期宣传专刊的主题,想知道学生对伦敦奥运会火炬传递路线的了解程度,决定随机抽取部分学生进行一次问卷调查,并根据收集到的信息进行了统计,绘制了如图两幅上不完整的统计图.请你根据统计图中所提供的信息解答下列问题: 
(1)接受问卷调查的学生共有名;
(2)请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小;
(3)若该校共有1200名学生,请根据上述调查结果估计该校学生中对伦敦奥运火炬传递路线达到了“了解”和“基本了解”程度的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( ) 
A.![]()
B.![]()
C.1
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD= ![]() ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作 ![]() ,交OB于E点.
,交OB于E点.
(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com