
����Ŀ�����ڶ��κ���y=x2��3x+2��һ�κ���y=��2x+4����y=t��x2��3x+2��+��1��t������2x+4����Ϊ�����������ġ��������κ�����������t�Dz�Ϊ���ʵ������ͼ�����������E�����е�A��2��0����������E�ϵĵ�B����1��n�����������������
��1����t=2ʱ��������E�Ķ�����������
��2���жϵ�A�Ƿ���������E�ϣ�
��3����n��ֵ��
��4��ͨ����2���ͣ�3���������֪������tȡ�κβ�Ϊ���ʵ����������E�ܹ����㣬�������������� ��
��5�����κ���y=��3x2+5x+2�Ƕ��κ���y=x2��3x+2��һ�κ���y=��2x+4��һ�����������κ�����������ǣ����t��ֵ��������ǣ�˵�����ɣ�
��6����ABΪһ��������ABCD��ʹ������һ����������y���ϣ���������E������A��B��C��D�е����㣬������з���������t��ֵ��
���𰸡�
��1����1����2��
��2��
�⣺��x=2����y=t��x2��3x+2��+��1��t������2x+4������ y=0��
���A��2��0����������E��
��3��
�⣺��x=��1����������E�Ľ���ʽ�У��ã�
n=t��x2��3x+2��+��1��t������2x+4��=6
��4��A��2��0����B����1��6��
��5��
�⣺��x=2����y=��3x2+5x+2��y=0������A���������ϣ�
��x=��1����y=��3x2+5x+2������ã�y=��6��6��
���ɵ�������y=��3x2+5x+2��������B��
���κ���y=��3x2+5x+2���Ƕ��κ���y=x2��3x+2��һ�κ���y=��2x+4��һ�����������κ�����
��6��
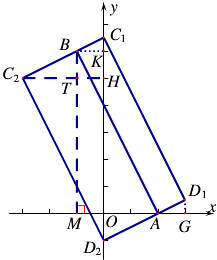
�⣺��ͼ��������ABC1D1��ABC2D2������B��BK��y���ڵ�K����B��BM��x���ڵ�M��
��AM=3��BM=6��BK=1����KBC1�ס�MBA��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() ����� C1K=
����� C1K= ![]() �����Ե�C1��0��
�����Ե�C1��0�� ![]() ����
����
��֪��KBC1�ա�GAD1����AG=1��GD1= ![]() ��
��
���D1��3�� ![]() ����
����
��֪��OAD2�ס�GAD1�� ![]() =
= ![]() ����AG=1��OA=2��GD1=
����AG=1��OA=2��GD1= ![]() ����� OD2=1�����D2��0����1����
����� OD2=1�����D2��0����1����
��֪��TBC2�ա�OD2A����TC2=AO=2��BT=OD2=1�����Ե�C2����3��5����
��������E�ܹ�����A��2��0����B����1��6����
��������������������A��B��C��A��B��D��
��������E����A��B��C1ʱ����C1��0�� ![]() ������y=t��x2��3x+2��+��1��t������2x+4�������t1=��
������y=t��x2��3x+2��+��1��t������2x+4�������t1=�� ![]() ��
��
��������E����A��B��D1��A��B��C2��A��B��D2ʱ���ɷֱ����t2= ![]() ��t3=��
��t3=�� ![]() ��t4=
��t4= ![]() ��
��
����������������t��ֵΪ���� ![]() ��
�� ![]() ����
���� ![]() ��
�� ![]() ��
��
���������⣺��1����t=2����������E�У��ã�y=t��x2��3x+2��+��1��t������2x+4��=2x2��4x=2��x��1��2��2��
���ʱ�����ߵĶ�������Ϊ����1����2����
4����������E�Ľ���ʽչ�����ã�
y=t��x2��3x+2��+��1��t������2x+4��=t��x��2����x+1����2x+4
��������E�ع����㣨2��0��������1��6����
�����㾫�������ն��κ�����ͼ��Ͷ��κ����������ǽ����ĸ�������Ҫ֪�����κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijְҵ���л�����ѧ��42�ˣ���������������Ů��������2����3�ˣ�
��1���ð�������Ů�����ж����ˣ�
��2��ij�����������ð���¼30��ѧ���������ԣ��ð��С�Ů��ÿ���ܼӹ���������ֱ�Ϊ50����45����Ϊ��֤����ÿ��ӹ����������������1460������ô����Ҫ��¼��������ѧ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ĵ�����װ�д�С���ʵ���ȫ��ͬ��3ֻ�����Ϸֱ����2��3��5�������֣�
��1�������������������һֻ�����������������ĸ�������
��2�������������������һֻ�����������֣����Żأ��ٴӴ����������������һֻ�����������֣�����һ�μ��µ�������Ϊʮλ���֣��ڶ��μ��µ�������Ϊ��λ���֣����һ����λ����������ɵ���λ����5�ı����ĸ��ʣ������á�����״ͼ�����б����ķ���д�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��AB������A����4��0����B��0��4������O�İ뾶Ϊ1��OΪ����ԭ�㣩����P��ֱ��AB�ϣ�����P����O��һ������PQ��QΪ�е㣬�����߳�PQ����СֵΪ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ�ٰ조�������Ļ��С��Ϊ�˴λ�����һ��������ɽΪ������ͼ�꣨��ͼ�������ú졢��������ɫ��ͼ���е�A��B��C��������������ֱ�Ϳɫ��һ������ֻͿһ����ɫ�� 
��1��������״ͼ�г�����Ϳɫ�Ŀ��ܽ����
��2������������������������Ϳ��ɫ�ǡ������ɫ��һ���ɫ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��˫����y= ![]() ����Rt��OMNб���ϵĵ�A����ֱ�DZ�MN�ཻ�ڵ�B����֪OA=2AN����OAB�����Ϊ5����k��ֵ��
����Rt��OMNб���ϵĵ�A����ֱ�DZ�MN�ཻ�ڵ�B����֪OA=2AN����OAB�����Ϊ5����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�����OABC�Ķ���O������ԭ�㣬����A��C�ֱ���x�ᡢy����������ϣ���OA=2��OC=1�����ζԽ���AC��OB�ཻ��E������E��ֱ�����OA��BC�ֱ��ཻ�ڵ�G��H�� 
��1��ֱ��д����E�����꣺ ��
��2����֤��AG=CH��
��3����ͼ2����OΪԲ�ģ�OCΪ�뾶��Բ����OA��D����ֱ��GH�뻡CD���ڵ�Բ�����ھ�����һ��F����ֱ��GH�ĺ�����ϵʽ�� 
��4���ڣ�3���Ľ����£�����ABHG���ڲ���һ��P������P��HG��GA��AB������ʱ�����P�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̫���ܹ���������ִ���ɫ��������֮һ�����������Լ��ݶ��Ľ��ɹ�����棬�Ľ�ǰ�ݶ������ABC��ͼ2��ʾ��BC=10�ף���ABC=��ACB=36�㣬�Ľ���D��BA���ӳ����ϣ��ҡ�BDC=90�㣬��Ľ���������������Ӳ���AD�ij����������ȷ��0.1�ף�
���ο����ݣ�sin18���0.31��cos18���0.95��tan18���0.32��sin36���0.59��cos36���0.81��tan36���0.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+2x+6��a��0����x����A��B���㣨��A�ڵ�B��ࣩ����ֱ��WXYZ��x�Ḻ�����45����ã���WZ�����������ϵĵ�C��4��m�����������ߵ���һ����Ϊ��D��ֱ�߱�x��صõ��߶�EF=2���ҡ�CEF�����Ϊ6��
��1����������ߵĽ���ʽ��
��2��̽������ֱ��AC�Ϸ������������Ƿ����һ��P��ʹ�á�ACP�������������ڣ��������������ֵ����ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
��3����ֱ����ÿ��2����λ���ٶ���x������ƽ�ƣ���ƽ�Ƶ�ʱ��Ϊt�룬ƽ�ƺ��ֱ��ΪW��X��Y��Z�䣬���б�X��Y�����ڵ�ֱ����x�ύ�ڵ�M���������ߵ�����һ������Ϊ��N����ֱ��д����tΪ��ֵʱ����ʹ����C��D��M��NΪ������ı�����ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com