
【题目】对x,y定义一种新运算T,规定:![]() (其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:
(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:![]() .
.
(1)已知T(1,﹣1)=﹣2,T(4,2)=1.
①求a、b的值;
②若关于m的方程T(1﹣m,﹣m2)=﹣2有实数解,求实数m的值;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a、b应满足怎样的关系式?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】 我们已经学习了利用配方法解一元二次方程,其实配方法还有其它重要应用.
例:已知x可取任何实数,试求二次三项式2x2-12x+14的值的范围.
解:2x2-12x+14=2(x2-6x)+14=2(x2-6x+32-32)+14
=2[(x-3)2-9]+14=2(x-3)2-18+14=2(x-3)2-4.
∵无论x取何实数,总有(x-3)2≥0,∴2(x-3)2-4≥-4.
即无论x取何实数,2x2-12x+14的值总是不小于-4的实数.
问题:已知x可取任何实数,则二次三项式-3x2+12x-11的最值情况是( )
A.有最大值-1 B.有最小值-1 C.有最大值1 D.有最小值1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=![]() (x>0)的图象经过点A、B,点A的坐标为(1,2),过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC、OD.
(x>0)的图象经过点A、B,点A的坐标为(1,2),过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC、OD.

(1)求△OCD的面积;
(2)当BE=![]() AC时,求CE的长.
AC时,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(![]() ,1)、B(2,0)、O(0,0),反比例函数y=
,1)、B(2,0)、O(0,0),反比例函数y=![]() 图象经过点A.
图象经过点A.

(1)求k的值;
(2)将△AOB绕点O逆时针旋转60°,得到△COD,其中点A与点C对应,试判断点D是否在该反比例函数的图象上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P′是由点P(2,3)先向右平移3个单位,再向下平移2个单位得到的,则点P′的坐标是( )
A. (5,5) B. (﹣1,1) C. (5,1) D. (﹣1,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
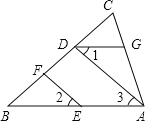
【题目】按图填空,并注明理由.
如图,在△ABC中,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:因为EF∥AD(已知)
所以∠2=∠3.( )
又因为∠1=∠2,所以∠1=∠3.(等量代换)
所以AB∥ ( )
所以∠BAC+ =180°( ).
又因为∠BAC=70°,所以∠AGD=110°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点E为BC边上一动点(不与点B、C重合),过点E作射线EF交AC于点F,使∠AEF=∠B.

(1)判断∠BAE与∠CEF的大小关系,并说明理由;
(2)请你探索:当△AEF为直角三角形时,求∠AEF与∠BAE的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com