Question

【题目】如图，在△ABC中，AB=AC，点E为BC边上一动点（不与点B、C重合），过点E作射线EF交AC于点F，使∠AEF=∠B．

（1）判断∠BAE与∠CEF的大小关系，并说明理由；

（2）请你探索：当△AEF为直角三角形时，求∠AEF与∠BAE的数量关系．

Answer 1

【答案】（1）∠BAE=∠FEC（2）2∠AEF与∠BAE的数量关系是互余

【解析】

试题分析：（1）根据三角形内角与外角的关系可得∠B+∠BAE=∠AEC=∠AEF+∠FEC，再由条件∠AEF=∠B可得∠BAE=∠FEC；

（2）分别根据当∠AFE=90°时，以及当∠EAF=90°时利用外角的性质得出即可．

解：（1）∠BAE=∠FEC；

理由如下：

∵∠B+∠BAE=∠AEC，∠AEF=∠B，

∴∠BAE=∠FEC；

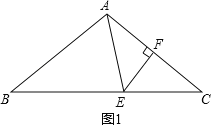
（2）如图1，当∠AFE=90°时，

∵∠B+∠BAE=∠AEF+∠CEF，

∠B=∠AEF=∠C，

∴∠BAE=∠CEF，

∵∠C+∠CEF=90°，

∴∠BAE+∠AEF=90°，

即∠AEF与∠BAE的数量关系是互余；

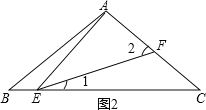
如图2，当∠EAF=90°时，

∵∠B+∠BAE=∠AEF+∠1，

∠B=∠AEF=∠C，

∴∠BAE=∠1，

∵∠C+∠1+∠AEF=90°，

∴2∠AEF+∠1=90°，

即2∠AEF与∠BAE的数量关系是互余．