
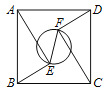
【题目】如图,正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=4,BE=DF=3,则以EF为直径的圆的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
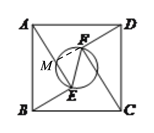
【解析】如图,延长DF交AE于点M,
∵正方形ABCD中,AD=AB=DC=5,AE=FC=4,BE=DF=3,
∴△ABE≌△CDF(SSS),AB2=AE2+BE2,CD2=FC2+DF2,
∴∠AEB=∠CFD=90°,∠BAE=∠DCF,
∴∠BAE+∠ABE=∠BAE+∠DAM=90°,∠DCF+∠CDF=∠ADF+∠CDF=90°,
∴∠ABE=∠DAM,∠ADF=∠DCF=∠BAE,
又∵AB=AD,
∴△ABE≌△DAM(ASA),
∴AM=BE=3,DM=AE=4,∠AMD=∠BEA=90°,
∴ME=AE-AM=4-3-1,MF=DM-DF=4-3=1,∠DME=90°,
∴EF=![]() ,
,
∴以EF为直径的圆的面积为: 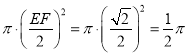 .
.
故选A.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
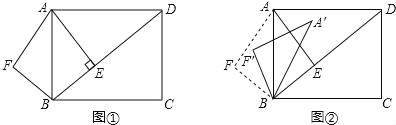
【题目】已知:如图①,在矩形ABCD中,AB=5,AD=![]() ,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
(1)求AE和BE的长;
(2)若将△ABF沿着射线BD方向平移,设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).当点F分别平移到线段AB、AD上时,直接写出相应的m的值;
(3)如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AD交于点P.与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列所给的各组线段,能组成三角形的是( )
A. 10cm、20cm、30cm B. 20cm、30cm、40cm
C. 10cm、20cm、40cm D. 10cm、40cm、50cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃2、3、4三张牌,抽取方式及规则不变,乙的方案公平吗?(只回答,不说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知矩形A的长、宽分别是2和1,那么是否存在另一个矩形B,它的周长和面积分别是矩形A的周长和面积的2倍?对上述问题,小明同学从“图形”的角度,利用函数图象给予了解决.小明论证的过程开始是这样的:如果用x、y分别表示矩形的长和宽,那么矩形B满足x+y=6,xy=4.请你按照小明的论证思路完成后面的论证过程.(画图并简单的文字说明)
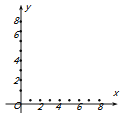
(2)已知矩形A的长和宽分别是2和1,那么是否存在一个矩形C,它的周长和面积分别是矩形A的周长和面积的一半?小明认为这个问题是肯定的,你同意小明的观点吗?为什么?(同上要求)
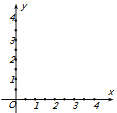
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本中有一道作业题:
有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题:
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
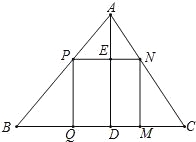
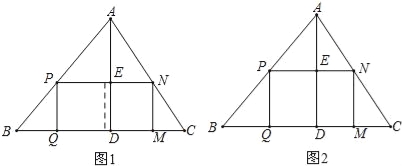
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com