
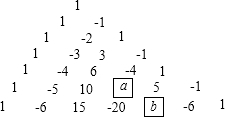
分析 由数列可知:(1)第n行共有n个数;
(2)每一行第一个数字为1,奇数位上的数字为正,偶数为上的数字为负,数字为它上方与它相邻两数绝对值得和;
(3)根据规律可求得a与b的值.
解答 解:(1)第2行共2个数,第5行共有5个数,第8行共有8个数,第n行共有n个数;
(2)有数列可知:每一行第一个数字为1,最后一个在数奇数行时为1,偶数行为-1,并且奇数位上的数字为正,偶数位上的数字为负,数字为它上方与它相邻两数绝对值得和,
因此第8行最左边的数是1,最右边的数是-1,第8行从左往右的第2个数是-8;
(3)有以上可知a=-10,b=15.
故答案为:(1)2,5,8,n;(2)1,-1,-8;(3)-10,15.
点评 本题考查了数字的变化规律.通过观察得出每一行数字的排列规律是解决此题的关键.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=26°,则∠CDE=71°.
如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=26°,则∠CDE=71°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
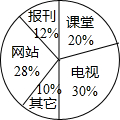 钓鱼岛是我国固有领土.某校七年级(15)班举行“爱国教育”为主题班会时,就有关钓鱼岛新闻的获取途径,对本班50名学生进行调查(要求每位同学,只选自己最认可的一项),并绘制如图所示的扇形统计图.
钓鱼岛是我国固有领土.某校七年级(15)班举行“爱国教育”为主题班会时,就有关钓鱼岛新闻的获取途径,对本班50名学生进行调查(要求每位同学,只选自己最认可的一项),并绘制如图所示的扇形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com