
分析 (1)利用二次根式的乘法运算法则以及零指数幂的性质化简求出即可;
(2)首先化简二次根式进而合并求出即可;
(3)利用负整数幂的性质以及二次根式的除法运算法则化简求出即可;
(4)利用积的乘方运算以及绝对值和零指数幂的性质化简求出即可.
解答 解:(1)$\sqrt{8}×\sqrt{\frac{1}{2}}+{(\sqrt{2})^0}$
=2$\sqrt{2}$×$\sqrt{\frac{1}{2}}$+1
=3;
(2)$(\sqrt{48}-4\sqrt{\frac{1}{8}})-(3\sqrt{\frac{1}{3}}-2\sqrt{0.5})$
=4$\sqrt{3}$-$\sqrt{2}$-$\sqrt{3}$+$\sqrt{2}$
=3$\sqrt{3}$;
(3)${(\frac{1}{{\sqrt{6}}})^{-2}}+\sqrt{20}÷\sqrt{5}$
=$\frac{1}{(\frac{1}{\sqrt{6}})^{2}}$+2
=8;
(4)${(2-\sqrt{3})^{2013}}•{(2+\sqrt{3})^{2014}}-2|{-\frac{{\sqrt{3}}}{2}}|-{(-\sqrt{3})^0}$
=[(2-$\sqrt{3}$)(2+$\sqrt{3}$)]2013(2+$\sqrt{3}$)-$\sqrt{3}$-1
=1.
点评 此题主要考查了二次根式的混合运算以及零指数幂的性质、积的乘方运算等知识,正确化简二次根式是解题关键.


科目:初中数学 来源: 题型:选择题
| 人数 | 3 | 4 | 2 | 1 |
| 分数 | 80 | 85 | 90 | 95 |
| A. | 85和82.5 | B. | 85.5和85 | C. | 85和85 | D. | 85.5和80 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
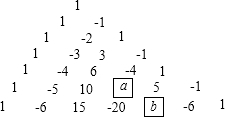
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3.则EC=5,AB=6.
如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3.则EC=5,AB=6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com