
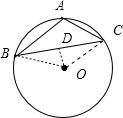
 解:当点O在△ABC的外部,如图,连OC,
解:当点O在△ABC的外部,如图,连OC, ×276°=138°;
×276°=138°; 连OC,
连OC, ∠BOC=42°.
∠BOC=42°.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
 如图,BE是△ABC的外接⊙O的直径,CD是△ABC的高.
如图,BE是△ABC的外接⊙O的直径,CD是△ABC的高.| AC |
| BE |
| DC |
| BC |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,⊙O是△ABC的
如图,⊙O是△ABC的查看答案和解析>>
科目:初中数学 来源:第28章《锐角三角函数》中考题集(24):28.2 解直角三角形(解析版) 题型:填空题
 ,则圆O的直径AE= .
,则圆O的直径AE= .
查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《圆》(12)(解析版) 题型:填空题
 ,则圆O的直径AE= .
,则圆O的直径AE= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com