
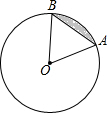
 如图,⊙O的半径为2,AB是⊙O的一条弦,∠O=60°,则图中阴影弓形的面积为
如图,⊙O的半径为2,AB是⊙O的一条弦,∠O=60°,则图中阴影弓形的面积为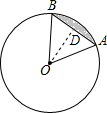 解:过点O作OD⊥AB于点D,
解:过点O作OD⊥AB于点D,
| ||
| 2 |
| 3 |
60π×22-
| ||||
| 360 |
240π-
| ||
| 360 |
| 4 |
| 5 |
| ||
| 360 |
| 4 |
| 5 |
| ||
| 360 |


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
 如图,是一个底面半径为1cm,高度为2πcm的无盖圆柱形玻璃容器,A、B两点在容器顶部一条直径的两端,现有一只小甲虫在容器外A点正下方1cm的M处,要爬到容器内B点正下方距离底部1cm的N处,则这只小甲虫最短爬行的距离是
如图,是一个底面半径为1cm,高度为2πcm的无盖圆柱形玻璃容器,A、B两点在容器顶部一条直径的两端,现有一只小甲虫在容器外A点正下方1cm的M处,要爬到容器内B点正下方距离底部1cm的N处,则这只小甲虫最短爬行的距离是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数y=
如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数y=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
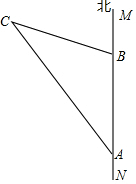 如图,直线MN是沿海边南北方向的一条公路,某施工队在公路的A点测得北偏西30°的方向上有一栋别墅C,沿正北方向走了400米到达B点后,测得别墅C在北偏西75°的方向上,现要从别墅C修一条通向公路MN的最短的小路,请你求出这条小路的长.
如图,直线MN是沿海边南北方向的一条公路,某施工队在公路的A点测得北偏西30°的方向上有一栋别墅C,沿正北方向走了400米到达B点后,测得别墅C在北偏西75°的方向上,现要从别墅C修一条通向公路MN的最短的小路,请你求出这条小路的长.查看答案和解析>>
科目:初中数学 来源: 题型:
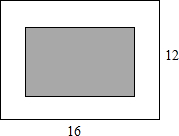 如图,计划在长为16m、宽为12m的矩形会议室的地面上铺设一个矩形地毯,若四周未铺地毯地面的宽度相同,且地毯面积占整个会议室地面面积的一半,求地毯的长与宽.
如图,计划在长为16m、宽为12m的矩形会议室的地面上铺设一个矩形地毯,若四周未铺地毯地面的宽度相同,且地毯面积占整个会议室地面面积的一半,求地毯的长与宽.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一架长为2.5m的梯子斜靠在竖直的墙上,梯子的底部离墙0.7m,若梯子的顶部滑下0.4m,则梯子的底部向外滑出( )
如图,一架长为2.5m的梯子斜靠在竖直的墙上,梯子的底部离墙0.7m,若梯子的顶部滑下0.4m,则梯子的底部向外滑出( )| A、1.5m | B、0.8m |
| C、0.4m | D、0.9m |
查看答案和解析>>
科目:初中数学 来源: 题型:
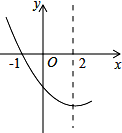 如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).有下列结论:①abc>0;②4a-2b+c<0;③b2-4ac>0’④点(-2,y1),(3,y2)都在抛物线上,则有y1<y2;⑤关于x的方程ax2+bx+c=0的解是-1和5.其中正确的是( )
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).有下列结论:①abc>0;②4a-2b+c<0;③b2-4ac>0’④点(-2,y1),(3,y2)都在抛物线上,则有y1<y2;⑤关于x的方程ax2+bx+c=0的解是-1和5.其中正确的是( )| A、①②③ | B、②④⑤ |
| C、①③⑤ | D、③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com