
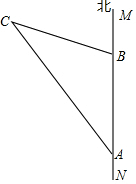
 如图,直线MN是沿海边南北方向的一条公路,某施工队在公路的A点测得北偏西30°的方向上有一栋别墅C,沿正北方向走了400米到达B点后,测得别墅C在北偏西75°的方向上,现要从别墅C修一条通向公路MN的最短的小路,请你求出这条小路的长.
如图,直线MN是沿海边南北方向的一条公路,某施工队在公路的A点测得北偏西30°的方向上有一栋别墅C,沿正北方向走了400米到达B点后,测得别墅C在北偏西75°的方向上,现要从别墅C修一条通向公路MN的最短的小路,请你求出这条小路的长.| 1 |
| 2 |
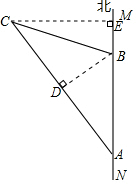 解:作BD⊥AC于点D,作CE⊥AB于点E,
解:作BD⊥AC于点D,作CE⊥AB于点E,| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:初中数学 来源: 题型:
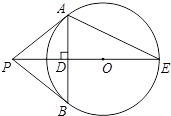 如图,PB切⊙O于点B,联结PO并延长交⊙O于点E,过点B作BA⊥PE交⊙O于点A,联结AP,AE.
如图,PB切⊙O于点B,联结PO并延长交⊙O于点E,过点B作BA⊥PE交⊙O于点A,联结AP,AE.| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| •• |
| 15 |
| 22 |
| 7 |
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知二次函数y=x2+bx+c的图象经过点(-4,3)、(-3,0).
已知二次函数y=x2+bx+c的图象经过点(-4,3)、(-3,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com