
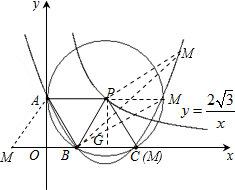
在直角坐标系xOy中,已知点P是反比例函数y= (x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:
①求出点A,B,C的坐标.
②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的 ?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.
?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.
(1) 四边形OKPA是正方形;(2)A(0, ),B(1,0),C(3,0);(3);(0,
),B(1,0),C(3,0);(3);(0, ),(3,0),(4,
),(3,0),(4, ),(7,8
),(7,8 ).
).
解析试题分析:(1)四边形OKPA是正方形.当⊙P分别与两坐标轴相切时,PA⊥y轴,PK⊥x轴,x轴⊥y轴,且PA=PK,可判断结论;
(2)①连接PB,设点P(x,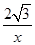 ),过点P作PG⊥BC于G,则半径PB=PC,由菱形的性质得PC=BC,可知△PBC为等边三角形,在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=
),过点P作PG⊥BC于G,则半径PB=PC,由菱形的性质得PC=BC,可知△PBC为等边三角形,在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=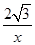 ,利用sin∠PBG=
,利用sin∠PBG=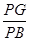 ,列方程求x即可;
,列方程求x即可;
②求直线PB的解析式,利用过A点或C点且平行于PB的直线解析式与抛物线解析式联立,列方程组求满足条件的M点坐标即可.
(1)四边形OKPA是正方形.
证明:∵⊙P分别与两坐标轴相切,
∴PA⊥OA,PK⊥OK.
∴∠PAO=∠OKP=90°.
又∵∠AOK=90°,
∴∠PAO=∠OKP=∠AOK=90°.
∴四边形OKPA是矩形.
又∵AP=KP,
∴四边形OKPA是正方形.
(2)①连接PB,设点P的横坐标为x,则其纵坐标为 .
.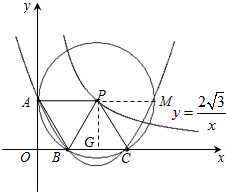
过点P作PG⊥BC于G.
∵四边形ABCP为菱形,
∴BC=PA=PB=PC(半径).
∴△PBC为等边三角形.
在Rt△PBG中,∠PBG=60°,PB=PA=x,
PG= sin∠PBG=
sin∠PBG=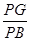 ,即
,即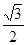 =
=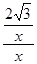 .
.
解之得:x=±2(负值舍去).
∴PG= ,PA=BC=2.P(2,
,PA=BC=2.P(2,  )
)
易知四边形OGPA是矩形,PA=OG=2,BG=CG=1,
∴OB=OG-BG=1,OC=OG+GC=3.
∴A(0, ),B(1,0),C(3,0).
),B(1,0),C(3,0).
②设二次函数解析式为:y=ax2+bx+c.
据题意得: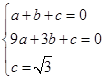
解之得: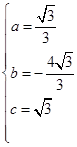 .
.
∴二次函数关系式为:y=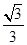 x2?
x2?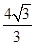 x+
x+ 
设直线BP的解析式为:y=ux+v,据题意得: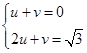 解之得:
解之得: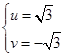 .
.
∴直线BP的解析式为:y=  x-
x- ,
,
过点A作直线AM∥BP,则可得直线AM的解析式为:y= x+
x+ .
.
解方程组: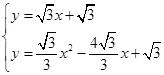
得: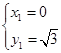 ;
;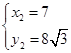 .
.
过点C作直线CM∥PB,则可设直线CM的解析式为:y= x+t.
x+t.
∴0=3 +t.
+t.
∴t=?3 .
.
∴直线CM的解析式为:y= x?3
x?3 .
.
解方程组: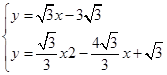
得: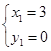 ;
;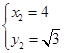 ..
..
综上可知,满足条件的M的坐标有四个,分别为:(0, ),(3,0),(4,
),(3,0),(4, ),(7,8
),(7,8 ).
).
考点: 二次函数综合题.


科目:初中数学 来源: 题型:解答题
如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于C点,点D在抛物线上且横坐标为3.
(1)求tan∠DBC的值;
(2)点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线y=x²+bx+c与直线y=x-1交于A、B两点.点A的横坐标为-3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
(1)求抛物线的解析式;
(2)当m为何值时, ;
;
(3)是否存在点P,使△PAD是直角三角形,若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线
与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线 于点C;
于点C;
(1)求该抛物线的解析式;
(2)求点A关于直线 的对称点
的对称点 的坐标,判定点
的坐标,判定点 是否在抛物线上,并说明理由;
是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段 于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图, 已知抛物线 与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1)。
与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1)。
(1)求抛物线的解析式;
(2)点E是线段AC上一动点,过点E作DE⊥x轴于点D,连结DC,当△DCE的面积最大时,求点D的坐标;
(3)在直线BC上是否存在一点P,使△ACP为等腰三角形,若存在,求点P的坐标,若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点A坐标为(-1,0).则下面的四个结论:
①2a+b=0;②4a+2b+c>0;③B点坐标为(4,0);④当x<-1时,y>0.
其中正确的是( )
A.①② B.③④ C.①④ D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知关于 的一元二次方程
的一元二次方程 .
.
(1)求证:方程总有两个实数根;
(2)若m为整数,当此方程有两个互不相等的负整数根时,求m的值;
(3)在(2)的条件下,设抛物线 与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP=
与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP= BC,求点P的坐标.
BC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
心理学家通过实验发现:初中学生听讲的注意力随时间变化,讲课开始时,学生注意力逐渐增强,中间有一段平稳状态,随后开始分散.学生注意力指标数y随时间表t(分钟)变化的函数图象如下.当0≤t≤10时,图像是抛物线的一部分,当10≤t≤20时和20≤t≤40时,图像是线段。
(1)当0≤t≤10时,求注意力指标数y与时间t的函数关系式;
(2)一道数学探究题需要讲解24分钟,问老师能否经过恰当安排,使学生在探究这道题时,注意力指标数不低于45?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在如图的直角坐标系中,已知点A(2,0)、B(0,-4),将线段AB绕点A按逆时针方向旋转90°至AC.
(1)求点C的坐标;
(2)若抛物线y=-x2+ax+4经过点C.
①求抛物线的解析式;
②在抛物线上是否存在点P(点C除外)使△ABP是以AB为直角边的等腰直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com