
如图,抛物线 与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线
与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线 于点C;
于点C;
(1)求该抛物线的解析式;
(2)求点A关于直线 的对称点
的对称点 的坐标,判定点
的坐标,判定点 是否在抛物线上,并说明理由;
是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段 于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
(1)抛物线的解析式为 .
.
(2)点A/的坐标为(﹣3,4),点A/在该抛物线上,理由见解析.
(3)存在,当点P运动到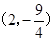 时,四边形PACM是平行四边形.理由见解析.
时,四边形PACM是平行四边形.理由见解析.
解析试题分析:(1)把A(5,0)、B(-1,0)两点代入二次函数解析式 中,解方程组得到b、c的值,即可求得抛物线的解析式.
中,解方程组得到b、c的值,即可求得抛物线的解析式.
(2)过点 作
作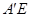 ⊥x轴于E,AA/与OC交于点D,可证得
⊥x轴于E,AA/与OC交于点D,可证得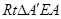 ∽
∽ ;再由相似三角形对应边成比例,可以求得点A′的坐标.然后把点A的坐标代入抛物线的解析式
;再由相似三角形对应边成比例,可以求得点A′的坐标.然后把点A的坐标代入抛物线的解析式 ,验证点A′是否在抛物线上即可.
,验证点A′是否在抛物线上即可.
(3)存在.设直线 的解析式为y=kx+b,将点C和点A′的坐标代入直线方程,即可得到直线
的解析式为y=kx+b,将点C和点A′的坐标代入直线方程,即可得到直线 的解析式为
的解析式为 ;设点P的坐标为
;设点P的坐标为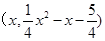 ,则点M为
,则点M为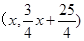 ,要使四边形PACM是平行四边形,只需PM=AC.又点M在点P的上方,则有
,要使四边形PACM是平行四边形,只需PM=AC.又点M在点P的上方,则有 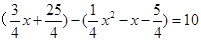 ,解此方程即可得到
,解此方程即可得到
点P的坐标.
试题解析:(1)∵ 与x轴交于A(5,0)、B(-1,0)两点,
与x轴交于A(5,0)、B(-1,0)两点,
∴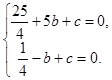 , 解得
, 解得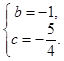
∴抛物线的解析式为 .························································3分
.························································3分
(2)过点 作
作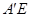 ⊥x轴于E,AA/与OC交于点D,
⊥x轴于E,AA/与OC交于点D,
∵点C在直线y=2x上, ∴C(5,10)
∵点A和 关于直线y=2x对称,
关于直线y=2x对称,
∴OC⊥ ,
,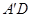 =AD.
=AD.
∵OA=5,AC=10,
∴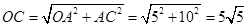 .
.
∵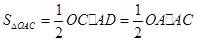 , ∴
, ∴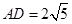 .∴
.∴ .·············5分
.·············5分
在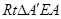 和Rt
和Rt 中,
中,
∵∠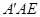 +∠
+∠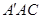 =90°,∠ACD+∠
=90°,∠ACD+∠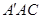 =90°,
=90°,
∴∠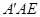 =∠ACD.
=∠ACD.
又∵∠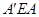 =∠OAC=90°,
=∠OAC=90°,
∴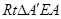 ∽
∽ .
.
∴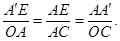 即
即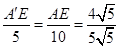 .
.
∴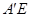 =4,AE=8.
=4,AE=8.
∴OE=AE-OA=3.
∴点A/的坐标为(﹣3,4).·······························7分
当x=﹣3时,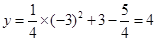 .
.
所以,点A/在该抛物线上.································8分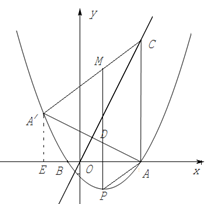
存在.
理由:设直线 的解析式为y=kx+b,
的解析式为y=kx+b,
则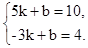 ,解得
,解得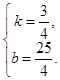
∴直线 的解析式为
的解析式为 .··················9分
.··················9分
设点P的坐标为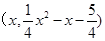 ,则点M为
,则点M为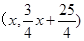 .
.
∵PM∥AC,
∴要使四边形PACM是平行四边形,只需PM=AC.又点M在点P的上方,
∴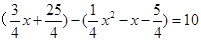 .
.
解得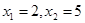 (不合题意,舍去)当x=2时,
(不合题意,舍去)当x=2时,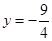 .
.
∴当点P运动到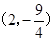 时,四边形PACM是平行四边形.····················11分
时,四边形PACM是平行四边形.····················11分
考点:二次函数综合题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
如图①,已知等腰梯形ABCD的周长为48,面积为S,AB∥CD,∠ADC=60°,设AB=3x.
(1)用x表示AD和CD;
(2)用x表示S,并求S的最大值;
(3)如图②,当S取最大值时,等腰梯形ABCD的四个顶点都在⊙O上,点E和点F分别是AB和CD的中点,求⊙O的半径R的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,直线 与抛物线
与抛物线 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图所示,已知二次函数 经过
经过 、
、 、C三点,点
、C三点,点 是抛物线与直线
是抛物线与直线 的一个交点.
的一个交点.
(1)求二次函数关系式和点C的坐标;
(2)对于动点 ,求
,求 的最大值;
的最大值;
(3)若动点M在直线 上方的抛物线运动,过点M做x轴的垂线交x轴于点F,如果直线AP把线段MF分成1:2的两部分,求点M的坐标。
上方的抛物线运动,过点M做x轴的垂线交x轴于点F,如果直线AP把线段MF分成1:2的两部分,求点M的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知直线AB: 与抛物线
与抛物线 交于A、B两点,
交于A、B两点,
(1)直线AB总经过一个定点C,请直接写出点C坐标;
(2)当 时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
(3)若在抛物线上存在定点D使∠ADB=90°,求点D到直线AB的最大距离.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,二次函数 的图象与
的图象与 轴交于
轴交于 、
、 两点,与
两点,与 轴交于
轴交于 点,已知点
点,已知点 (-1,0),点C(0,-2).
(-1,0),点C(0,-2).
(1)求抛物线的函数解析式;
(2)试探究 的外接圆的圆心位置,并求出圆心坐标;
的外接圆的圆心位置,并求出圆心坐标;
(3)此抛物线上是否存在点P,使得以P、A、C、B为顶点的四边形为梯形.若存在,请写出所有符合条件的P点坐标;若不存在,请说明理由;
(4)若点 是线段
是线段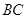 下方的抛物线上的一个动点,求
下方的抛物线上的一个动点,求 面积的最大值以及此时点
面积的最大值以及此时点 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在直角坐标系xOy中,已知点P是反比例函数y= (x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:
①求出点A,B,C的坐标.
②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的 ?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.
?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 交坐标轴于A、B、D三点,过点D作
交坐标轴于A、B、D三点,过点D作 轴的平行线交抛物线于点C.直线l过点E(0,-
轴的平行线交抛物线于点C.直线l过点E(0,-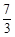 ),且平分梯形ABCD面积.
),且平分梯形ABCD面积.
⑴ 直接写出A、B、D三点的坐标;
⑵ 直接写出直线l的解析式;
⑶ 若点P在直线l上,且在x轴上方,tan∠OPB=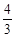 ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商家独家销售具有地方特色的某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x(x≥50)元/件的关系如下表:
| 销售单价x (元/件) | … | 55 | 60 | 70 | 75 | … |
| 一周的销售量y (件) | … | 450 | 400 | 300 | 250 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com