
如图①,已知等腰梯形ABCD的周长为48,面积为S,AB∥CD,∠ADC=60°,设AB=3x.
(1)用x表示AD和CD;
(2)用x表示S,并求S的最大值;
(3)如图②,当S取最大值时,等腰梯形ABCD的四个顶点都在⊙O上,点E和点F分别是AB和CD的中点,求⊙O的半径R的值.
(1)AD=18-2x,CD=16+x;(2)S=-2 (x-2)2+72
(x-2)2+72 ,当x=2时,S有最大值72
,当x=2时,S有最大值72 ;(3)R=2
;(3)R=2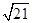 .
.
解析试题分析:(1)作AH⊥CD于H,BG⊥CD于G,如图①,易得四边形AHGB为矩形,则HG=AB=3x,再根据等腰梯形的性质得AD=BC,DH=CG,在Rt△ADH中,设DH=t,根据含30度的直角三角形三边的关系得AD=2t,AH= t,然后根据等腰梯形ABCD的周长为48得3x+2t+t+3x+t+2t=48,解得t=8-x,于是可得AD=18-2x,CD=16+x;
t,然后根据等腰梯形ABCD的周长为48得3x+2t+t+3x+t+2t=48,解得t=8-x,于是可得AD=18-2x,CD=16+x;
(2)根据梯形的面积公式计算可得到S=-2 x2+8
x2+8 x+64
x+64 ,再进行配方得S=-2
,再进行配方得S=-2 (x-2)2+72
(x-2)2+72 ,然后根据二次函数的最值问题求解;
,然后根据二次函数的最值问题求解;
(3)连结OA、OD,如图②,由(2)得到x=2时,则AB=6,CD=18,等腰梯形的高为6 ,所以AE=3,DF=9,由于点E和点F分别是AB和CD的中点,根据等腰梯形的性质得直线EF为等腰梯形ABCD的对称轴,所以EF垂直平分AB和CD,EF为等腰梯形ABCD的高,即EF=6
,所以AE=3,DF=9,由于点E和点F分别是AB和CD的中点,根据等腰梯形的性质得直线EF为等腰梯形ABCD的对称轴,所以EF垂直平分AB和CD,EF为等腰梯形ABCD的高,即EF=6 ,根据垂径定理的推论得等腰梯形ABCD的外接圆的圆心O在EF上,设OE=a,则OF=6
,根据垂径定理的推论得等腰梯形ABCD的外接圆的圆心O在EF上,设OE=a,则OF=6 -a,在Rt△AOE中,利用勾股定理得a2+32=R2,在Rt△ODF中,利用勾股定理得(6
-a,在Rt△AOE中,利用勾股定理得a2+32=R2,在Rt△ODF中,利用勾股定理得(6 -a)2+92=R2,然后消去R得到a的方程a2+32=(6
-a)2+92=R2,然后消去R得到a的方程a2+32=(6 -a)2+92,解得a=5
-a)2+92,解得a=5 ,最后利用R2=(5
,最后利用R2=(5 )2+32求解.
)2+32求解.
试题解析:(1)作AH⊥CD于H,BG⊥CD于G,如图①,
则四边形AHGB为矩形,
∴HG=AB=3x,
∵四边形ABCD为等腰梯形,
∴AD=BC,DH=CG,
在Rt△ADH中,设DH=t,
∵∠ADC=60°,
∴∠DAH=30°,
∴AD=2t,AH= t,
t,
∴BC=2t,CG=t,
∵等腰梯形ABCD的周长为48,
∴3x+2t+t+3x+t+2t=48,解得t=8-x,
∴AD=2(8-x)=18-2x,
CD=8-x+3x+8-x=16+x;
(2)S= (AB+CD)•AH
(AB+CD)•AH
= (3x+16+x)•
(3x+16+x)• (8-x)
(8-x)
=-2 x2+8
x2+8 x+64
x+64 ,
,
∵S=-2 (x-2)2+72
(x-2)2+72 ,
,
∴当x=2时,S有最大值72 ;
;
(3)连结OA、OD,如图②,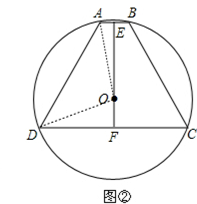
当x=2时,AB=6,CD=16+2=18,等腰梯形的高为 ×(8-2)=6
×(8-2)=6 ,
,
则AE=3,DF=9,
∵点E和点F分别是AB和CD的中点,
∴直线EF为等腰梯形ABCD的对称轴,
∴EF垂直平分AB和CD,EF为等腰梯形ABCD的高,即EF=6 ,
,
∴等腰梯形ABCD的外接圆的圆心O在EF上,
设OE=a,则OF=6 -a,
-a,
在Rt△AOE中,
∵OE2+AE2=OA2,
∴a2+32=R2,
在Rt△ODF中,
∵OF2+DF2=OD2,
∴(6 -a)2+92=R2,
-a)2+92=R2,
∴a2+32=(6 -a)2+92,解得a=5
-a)2+92,解得a=5 ,
,
∴R2=(5 )2+32=84,
)2+32=84,
∴R=2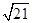 .
.
【考点】圆的综合题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
如图1,在平面直角坐标系xOy中,点M为抛物线 的顶点,过点(0,4)作x轴的平行线,交抛物线于点P、Q(点P在Q的左侧),PQ=4.
的顶点,过点(0,4)作x轴的平行线,交抛物线于点P、Q(点P在Q的左侧),PQ=4.
(1)求抛物线的函数关系式,并写出点P的坐标;
(2)小丽发现:将抛物线 绕着点P旋转180°,所得新抛物线的顶点恰为坐标原点O,你认为正确吗?请说明理由;
绕着点P旋转180°,所得新抛物线的顶点恰为坐标原点O,你认为正确吗?请说明理由;
(3)如图2,已知点A(1,0),以PA为边作矩形PABC(点P、A、B、C按顺时针的方向排列), .
.
①写出C点的坐标:C( , )(坐标用含有t的代数式表示);
②若点C在题(2)中旋转后的新抛物线上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1、2,已知四边形ABCD为正方形,在射线AC上有一动点P,作PE⊥AD(或延长线)于E,作PF⊥DC(或延长线)于F,作射线BP交EF于G.
(1)在图1中,设正方形ABCD的边长为2,四边形ABFE的面积为y,AP=x,求y关于x的函数表达式;
(2)结论:GB⊥EF对图1,图2都是成立的,请任选一图形给出证明;
(3)请根据图2证明:△FGC∽△PFB.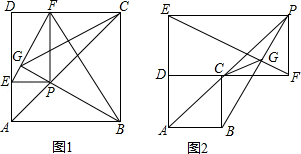
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
今年5月1日起实施《青海省保障性住房准入分配退出和运营管理实施细则》规定:公共租赁住房和廉租住房并轨运行(以下简称并轨房),计划10年内解决低收入人群住房问题.已知第x年(x为正整数)投入使用的并轨房面积为y百万平方米,且y与x的函数关系式为y=-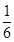 x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:
x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:
| 时间x(单位:年,x为正整数) | 1 | 2 | 3 | 4 | 5 | … |
| 单位面积租金z(单位:元/平方米) | 50 | 52 | 54 | 56 | 58 | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;
(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于C点,点D在抛物线上且横坐标为3.
(1)求tan∠DBC的值;
(2)点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
定义1:在△ABC中,若顶点A,B,C按逆时针方向排列,则规定它的面积为“有向面积”;若顶点A,B,C按顺时针方向排列,则规定它的面积的相反数为△ABC的“有向面积”.“有向面积”用 表示,例如图1中,
表示,例如图1中, ,图2中,
,图2中, .
.
定义2:在平面内任取一个△ABC和点P(点P不在△ABC的三边所在直线上),称有序数组( ,
, ,
, )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2, ,则
,则 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标” 为
为 .在图3中,我们知道
.在图3中,我们知道 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: .
.
应用新知:
(1)如图4,正方形ABCD的边长为1,则 ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现:
(2)在平面直角坐标系 中,点
中,点 ,
,
①若点P是第二象限内任意一点(不在直线AB上),设点P关于 的“面积坐标”为
的“面积坐标”为 ,
,
试探究 与
与 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;
②若点 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于 的“面积坐标”(用x,y表示);
的“面积坐标”(用x,y表示);
解决问题:
(3)在(2)的条件下,点 ,点Q在抛物线
,点Q在抛物线 上,求当
上,求当 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线
与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线 于点C;
于点C;
(1)求该抛物线的解析式;
(2)求点A关于直线 的对称点
的对称点 的坐标,判定点
的坐标,判定点 是否在抛物线上,并说明理由;
是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段 于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com