
如图,在平面直角坐标系中,直线 与抛物线
与抛物线 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,直接写出对应的点P的坐标.
(1)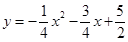 ;
;
(2)①x=﹣3时,l最大=15;
②点P有三个,分别是P1(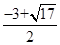 ,2),P2(
,2),P2( ,2),P3(
,2),P3(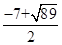 ,
,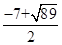 ).
).
解析试题分析:(1)利用待定系数法求出b,c即可;
(2)①根据△AOM∽△PED,得出DE:PE:PD=3:4:5,再求出PD=yP﹣yD求出二函数最值即可;
②当点G落在y轴上时,由△ACP≌△GOA得PC=AO=2,即 ,解得
,解得 ,
,
所以得出P点坐标,当点F落在y轴上时,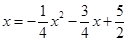 ,解得
,解得 ,可得P点坐标.
,可得P点坐标.
试题解析:(1)对于 ,当y=0,x=2.当x=﹣8时,y=﹣
,当y=0,x=2.当x=﹣8时,y=﹣ .
.
∴A点坐标为(2,0),B点坐标为(﹣8,﹣ ).
).
由抛物线 经过A、B两点,
经过A、B两点,
得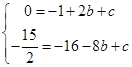
解得 .
.
∴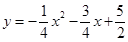 ;
;
(2)①设直线 与y轴交于点M,
与y轴交于点M,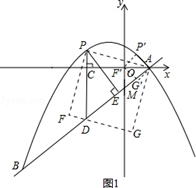
当x=0时,y= .∴OM=
.∴OM= .
.
∵点A的坐标为(2,0),∴OA=2.∴AM=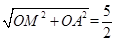 .
.
∵OM:OA:AM=3:4:5.
由题意得,∠PDE=∠OMA,∠AOM=∠PED=90°,∴△AOM∽△PED.
∴DE:PE:PD=3:4:5.
∵点P是直线AB上方的抛物线上一动点,
∵PD⊥x轴,
∴PD两点横坐标相同,
∴PD=yP﹣yD=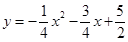 ﹣(
﹣(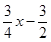 )=﹣
)=﹣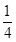 x2﹣
x2﹣ x+4,
x+4,
∴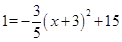 .
.
∴x=﹣3时,l最大=15;
②当点G落在y轴上时,如图2,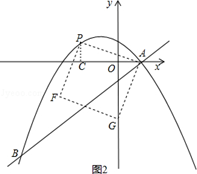
由△ACP≌△GOA得PC=AO=2,
即 ,解得
,解得 ,
,
所以P1(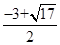 ,2),P2(
,2),P2( ,2),
,2),
如图3,过点P作PN⊥y轴于点N,过点P作PS⊥x轴于点S,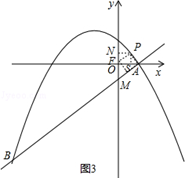
由△PNF≌△PSA,
PN=PS,可得P点横纵坐标相等,
故得当点F落在y轴上时,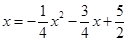 ,解得
,解得 ,
,
可得P3(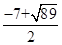 ,
,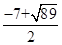 ),P4(
),P4(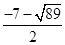 ,
,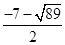 ),(舍去).
),(舍去).
综上所述:满足题意的点P有三个,分别是P1(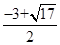 ,2),P2(
,2),P2( ,2),P3(
,2),P3(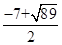 ,
,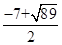 ).
).
考点:二次函数综合题.


科目:初中数学 来源: 题型:解答题
如图1,在平面直角坐标系xOy中,点M为抛物线 的顶点,过点(0,4)作x轴的平行线,交抛物线于点P、Q(点P在Q的左侧),PQ=4.
的顶点,过点(0,4)作x轴的平行线,交抛物线于点P、Q(点P在Q的左侧),PQ=4.
(1)求抛物线的函数关系式,并写出点P的坐标;
(2)小丽发现:将抛物线 绕着点P旋转180°,所得新抛物线的顶点恰为坐标原点O,你认为正确吗?请说明理由;
绕着点P旋转180°,所得新抛物线的顶点恰为坐标原点O,你认为正确吗?请说明理由;
(3)如图2,已知点A(1,0),以PA为边作矩形PABC(点P、A、B、C按顺时针的方向排列), .
.
①写出C点的坐标:C( , )(坐标用含有t的代数式表示);
②若点C在题(2)中旋转后的新抛物线上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于C点,点D在抛物线上且横坐标为3.
(1)求tan∠DBC的值;
(2)点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
定义1:在△ABC中,若顶点A,B,C按逆时针方向排列,则规定它的面积为“有向面积”;若顶点A,B,C按顺时针方向排列,则规定它的面积的相反数为△ABC的“有向面积”.“有向面积”用 表示,例如图1中,
表示,例如图1中, ,图2中,
,图2中, .
.
定义2:在平面内任取一个△ABC和点P(点P不在△ABC的三边所在直线上),称有序数组( ,
, ,
, )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2, ,则
,则 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标” 为
为 .在图3中,我们知道
.在图3中,我们知道 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: .
.
应用新知:
(1)如图4,正方形ABCD的边长为1,则 ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现:
(2)在平面直角坐标系 中,点
中,点 ,
,
①若点P是第二象限内任意一点(不在直线AB上),设点P关于 的“面积坐标”为
的“面积坐标”为 ,
,
试探究 与
与 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;
②若点 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于 的“面积坐标”(用x,y表示);
的“面积坐标”(用x,y表示);
解决问题:
(3)在(2)的条件下,点 ,点Q在抛物线
,点Q在抛物线 上,求当
上,求当 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线y= x+m与抛物线y=
x+m与抛物线y= x2-2x+l交于不同的两点M、N(点M在点N的左侧).
x2-2x+l交于不同的两点M、N(点M在点N的左侧).
(1)设抛物线的顶点为B,对称轴l与直线y= x+m的交点为C,连结BM、BN,若S△MBC=
x+m的交点为C,连结BM、BN,若S△MBC= S△NBC,求直线MN的解析式;
S△NBC,求直线MN的解析式;
(2)在(1)条件下,已知点P(t,0)为x轴上的一个动点,
①若△PMN为直角三角形,求点P的坐标.
②若∠MPN>90°,则t的取值范围是 .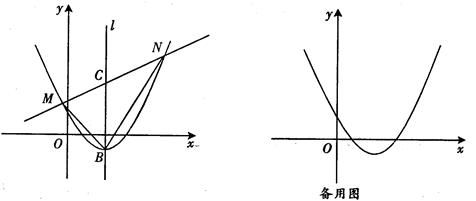
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
抛物线 (b,c均为常数)与x轴交于
(b,c均为常数)与x轴交于 两点,与y轴交于点
两点,与y轴交于点 .
.
(1)求该抛物线对应的函数表达式;
(2)若P是抛物线上一点,且点P到抛物线的对称轴的距离为3,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线y=x²+bx+c与直线y=x-1交于A、B两点.点A的横坐标为-3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
(1)求抛物线的解析式;
(2)当m为何值时, ;
;
(3)是否存在点P,使△PAD是直角三角形,若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线
与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线 于点C;
于点C;
(1)求该抛物线的解析式;
(2)求点A关于直线 的对称点
的对称点 的坐标,判定点
的坐标,判定点 是否在抛物线上,并说明理由;
是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段 于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
心理学家通过实验发现:初中学生听讲的注意力随时间变化,讲课开始时,学生注意力逐渐增强,中间有一段平稳状态,随后开始分散.学生注意力指标数y随时间表t(分钟)变化的函数图象如下.当0≤t≤10时,图像是抛物线的一部分,当10≤t≤20时和20≤t≤40时,图像是线段。
(1)当0≤t≤10时,求注意力指标数y与时间t的函数关系式;
(2)一道数学探究题需要讲解24分钟,问老师能否经过恰当安排,使学生在探究这道题时,注意力指标数不低于45?请通过计算说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com