
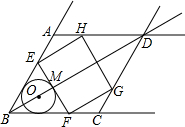
 如图,在射线BA,BC,AD,CD围成的菱形ABCD中,∠ABC=60°,AB=6$\sqrt{3}$,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上.
如图,在射线BA,BC,AD,CD围成的菱形ABCD中,∠ABC=60°,AB=6$\sqrt{3}$,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上.分析 (1)设⊙O切AB于点P,连接OP,由切线的性质可知∠OPB=90°.先由菱形的性质求得∠OBP的度数,然后依据含30°直角三角形的性质证明即可;
(2)设GH交BD于点N,连接AC,交BD于点Q.先依据特殊锐角三角函数值求得BD的长,设⊙O的半径为r,则OB=2r,MB=3r.当点E在AB上时.在Rt△BEM中,依据特殊锐角三角函数值可得到EM的长(用含r的式子表示),由图形的对称性可得到EF、ND、BM的长(用含r的式子表示,从而得到MN=18-6r,接下来依据矩形的面积列方程求解即可;当点E在AD边上时.BM=3r,则MD=18-3r,最后由MB=3r=12列方程求解即可;
(3)先根据题意画出符合题意的图形,①如图4所示,点E在AD上时,可求得DM=$\sqrt{3}$r,BM=3r,然后依据BM+MD=18,列方程求解即可;②如图5所示;依据图形的对称性可知得到OB=$\frac{1}{2}$BD;③如图6所示,可证明D与O重合,从而可求得OB的长;④如图7所示:先求得DM=$\sqrt{3}$r,OMB=3r,由BM-DM=DB列方程求解即可.
解答 解:(1)如图1所示:设⊙O切AB于点P,连接OP,则∠OPB=90°.
∵四边形ABCD为菱形,
∴∠ABD=$\frac{1}{2}$∠ABC=30°.
∴OB=2OP.
∵OP=OM,
∴BO=2OP=2OM.
(2)如图2所示:设GH交BD于点N,连接AC,交BD于点Q.
∵四边形ABCD是菱形,
∴AC⊥BD.
∴BD=2BQ=2AB•cos∠ABQ=$\sqrt{3}$AB=18.
设⊙O的半径为r,则OB=2r,MB=3r.
∵EF>HE,
∴点E,F,G,H均在菱形的边上.
①如图2所示,当点E在AB上时.
在Rt△BEM中,EM=BM•tan∠EBM=$\sqrt{3}$r.
由对称性得:EF=2EM=2$\sqrt{3}$r,ND=BM=3r.
∴MN=18-6r.
∴S矩形EFGH=EF•MN=2$\sqrt{3}$r(18-6r)=24$\sqrt{3}$.
解得:r1=1,r2=2.
当r=1时,EF<HE,
∴r=1时,不合题意舍
当r=2时,EF>HE,
∴⊙O的半径为2.
∴BM=3r=6.
如图3所示:
当点E在AD边上时.BM=3r,则MD=18-3r.
由对称性可知:NB=MD=6.
∴MB=3r=18-6=12.
解得:r=4.
综上所述,⊙O的半径为2或4.
(3)解设GH交BD于点N,⊙O的半径为r,则BO=2r.
当点E在边BA上时,显然不存在HE或HG与⊙O相切.
①如图4所示,点E在AD上时.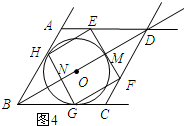
∵HE与⊙O相切,
∴ME=r,DM=$\sqrt{3}$r.
∴3r+$\sqrt{3}$r=18.
解得:r=9-3$\sqrt{3}$.
∴OB=18-6$\sqrt{3}$.
②如图5所示;
由图形的对称性得:ON=OM,BN=DM.
∴OB=$\frac{1}{2}$BD=9.
③如图6所示.
∵HG与⊙O相切时,MN=2r.
∵BN+MN=BM=3r.
∴BN=r.
∴DM=$\sqrt{3}$FM=$\sqrt{3}$GN=BN=r.
∴D与O重合.
∴BO=BD=18.
④如图7所示: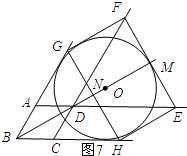
∵HE与⊙O相切,
∴EM=r,DM=$\sqrt{3}$r.
∴3r-$\sqrt{3}$r=18.
∴r=9+3$\sqrt{3}$.
∴OB=2r=18+6$\sqrt{3}$.
综上所述,当HE或GH与⊙O相切时,OB的长为18-6$\sqrt{3}$或9或18或18+6$\sqrt{3}$.
点评 本题主要考查的是四边形的综合应用,解答本题主要应用了菱形的性质、切线的性质、特殊锐角三角函数值的应用、矩形的面积公式,根据题意画出符合题意的图形是解题的关键.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段a.只用直尺(没有刻度的尺)和圆规,求作一个直角三角形ABC,以AB和BC分别为两条直角边,使AB=a,BC=$\frac{1}{2}$a(要求保留作图痕迹,不必写出作法)
如图,已知线段a.只用直尺(没有刻度的尺)和圆规,求作一个直角三角形ABC,以AB和BC分别为两条直角边,使AB=a,BC=$\frac{1}{2}$a(要求保留作图痕迹,不必写出作法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
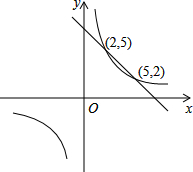 已知,如图一次函数y1=ax+b与反比例函数y2=$\frac{k}{x}$的图象如图示,当y1<y2时,x的取值范围是( )
已知,如图一次函数y1=ax+b与反比例函数y2=$\frac{k}{x}$的图象如图示,当y1<y2时,x的取值范围是( )| A. | x<2 | B. | x>5 | C. | 2<x<5 | D. | 0<x<2或x>5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com