
如图,在平行四边形ABCD中,E为BC边上的一点,且AE与DE分别平分 和
和

(1)求证: ;
;
(2)设以AD为直径的半圆交AB于F,连结DF交AE于G,已知CD=5,AE=8.
①求BC的长;
②求 值.
值.
(1)证明见解析;
(2)①BC =10; ②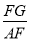 =
=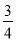 .
.
【解析】
试题分析:(1)由四边形ABCD是?,可知AB∥CD,那么就有∠BAD+∠ADC=180°,又AE、DE是∠BAD、∠ADC的角平分线,容易得出∠DAE+∠ADE=90°,即AE⊥DE;
(2)①由于AD∥BC,AE是角平分线,容易得∠BAE=∠BEA,那么AB=BE=CD=5,同理有CE=CD=5,容易得出BC =BE+CE=10;
②在Rt△ADE中,利用勾股定理可求DE,由于AD是直径,所以tan∠FAG=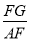 ,而∠FAG=∠DAE,于是
,而∠FAG=∠DAE,于是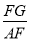 =
= ,即可求.
,即可求.
试题解析:(1)在平行四边形ABCD中,AB∥CD,
∴∠BAD+∠ADC=180°.
又∵AE、DE平分∠BAD、∠ADC,
∴∠DAE+∠ADE=90°,
∴∠AED=90°,
∴AE⊥DE;
(2)①在平行四边形ABCD中,AD∥BC,AB=CD=5,AD=BC,
∴∠DAE=∠BEA.
又∵∠DAE=∠BAE,
∴∠BEA=∠BAE,
∴BE=AB=5.
同理EC=CD=5.
∴BC= BE+EC=10;
②在平行四边形ABCD中,AD= BC= 10,
在Rt△AED中,DE=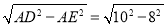 =6.
=6.
又∵AE是∠BAD的角平分线,
∴∠FAG=∠DAE.
∵AD是直径,
∴∠AFD=90°,
∴tan∠FAG=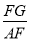 ,
,
∴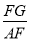 =tan∠DAE=
=tan∠DAE= =
=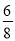 =
=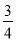 .
.
考点:1.平行四边形的性质2.圆周角定理3.解直角三角形.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源:2013-2014学年湖北省十堰市九年级4月调研考试数学试卷(解析版) 题型:解答题
如图,抛物线 与
与 交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①
交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:① ;②
;② 时,
时, ;③平行于x轴的直线
;③平行于x轴的直线 与两条抛物线有四个交点;④2AB=3AC.其中错误结论的个数是( )
与两条抛物线有四个交点;④2AB=3AC.其中错误结论的个数是( )

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省十堰市九年级4月调研考试数学试卷(解析版) 题型:选择题
下列计算正确的是( )
A.a2·a3=a6 B.a3÷a=a3
C.(-a2)3=-a6 D.(-2a2)4=8a8
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省杭州市拱墅区中考二模考试数学试卷(解析版) 题型:填空题
已知,如图双曲线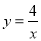 (x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线
(x>0)与直线EF交于点A,点B,且AE=AB=BF,连结AO,BO,它们分别与双曲线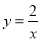 (x>0)交于点C,点D,则:
(x>0)交于点C,点D,则:
(1)AB与CD的位置关系是__________;
(2)四边形ABDC的面积为__________.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省杭州市拱墅区中考二模考试数学试卷(解析版) 题型:选择题
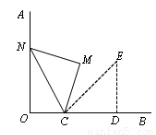
如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则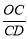 的值为( )
的值为( )
A.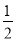 B.
B.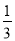 C.
C.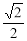 D.
D.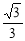
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江杭州十五中教育集团九年级第二学期3月月考数学试卷(解析版) 题型:填空题
已知函数y1=x,y2=x2和y3= ,有一个关于x的函数,不论x取何值,y的解析式总是取y1、 y2、y3中的值的较小的一个,则y的最大值等于
,有一个关于x的函数,不论x取何值,y的解析式总是取y1、 y2、y3中的值的较小的一个,则y的最大值等于
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河南省中考调考二数学试卷(解析版) 题型:解答题
某商店销售一种商品,每件的进价为2.5元,根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是13.5元时,销售量为500件,而单价每降低1元,就可以多售出200件.请你分析,销售单价多少时,可以获利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com